题目内容
【题目】如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为20m，如果水位上升3m时，水面CD的宽是10m．
（1）建立如图所示的直角坐标系，求此抛物线的解析式；
（2）现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地，已知甲地距此桥280km（桥长忽略不计）．货车正以每小时40km的速度开往乙地，当行驶1小时时，忽然接到紧急通知：前方连降暴雨，造成水位以每小时0.25m的速度持续上涨（货车接到通知时水位在CD处，当水位达到桥拱最高点O时，禁止车辆通行），试问：如果货车按原来速度行驶，能否安全通过此桥？若能，请说明理由；若不能，要使货车安全通过此桥，速度应超过每小时多少千米？
【答案】（1）抛物线的解析式为y=﹣
x2；
（2）要使货车安全通过此桥，货车的速度应超过60千米/时．
【解析】试题分析：根据抛物线在坐标系的位置，设抛物线的解析式为y=ax2，设D、B的坐标求解析式；
试题解析：（1）设抛物线的解析式为y=ax2（a不等于0），桥拱最高点O到水面CD的距离为h米．
则D（5，﹣h），B（10，﹣h﹣3）
∴
解得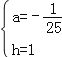
∴抛物线的解析式为y=﹣
x2
（2）水位由CD处涨到点O的时间为：1÷0.25=4（小时）
货车按原来速度行驶的路程为：40×1+40×4=200＜280
∴货车按原来速度行驶不能安全通过此桥．
设货车速度提高到x千米/时
当4x+40×1=280时，x=60
∴要使货车安全通过此桥，货车的速度应超过60千米/时．
练习册系列答案
相关题目
