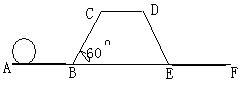题目内容
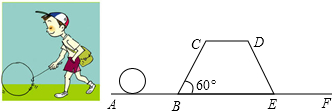
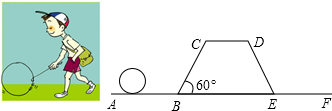
滚铁环是项深受大家喜爱的运动项目,铁环通常是用一根粗钢筋,弯成一个直径约40厘米的圆圈制成,然后用一个半圆的钩作“车把”,先将铁环向前转,然后拿“车把”赶快去推着向前走.小明同学在如图所示粗糙的平面轨道上滚动一个铁环,已知,AB与CD是水平的,BC与水平方向夹角为60°,四边形BCDE是等腰梯形,CD=EF=AB=BC=4m,小明将铁环从A点滚动至F点其圆心所经过的路线长度 .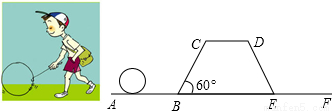
【答案】分析:根据题意画出铁环从A点滚动至F点其圆心所经过的路线为(AB+BC+CD+DE+EF)+2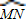 长-4HB,根据切线长定理及锐角三角函数定义,由GH的长,求出HB的长,由CD与BE平行,根据两直线平行同旁内角互补求出∠BCD的度数,进而求出∠MCN的度数,再由半径MC,利用弧长公式求出
长-4HB,根据切线长定理及锐角三角函数定义,由GH的长,求出HB的长,由CD与BE平行,根据两直线平行同旁内角互补求出∠BCD的度数,进而求出∠MCN的度数,再由半径MC,利用弧长公式求出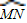 的长,代入表示出的路线中,即可求出铁环从A点滚动至F点其圆心所经过的路线长.
的长,代入表示出的路线中,即可求出铁环从A点滚动至F点其圆心所经过的路线长.
解答:解:根据题意画出圆心运动的轨迹,如图所示:
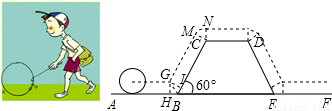
∵Rt△GHB中,GH=0.2米,∠GBH=∠GBI= ∠HBI=60°,
∠HBI=60°,
∴tan60°=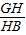 ,即HB=
,即HB=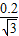 =
=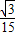 ,
,
∵CD∥BE,∠CBE=60°,
∴∠BCD=120°,
∴∠MCN=60°,又CM=0.2米,
∴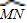 的长为
的长为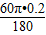 =
=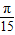 ,
,
∵圆的半径为20厘米=0.2米,CD=EF=AB=BC=4m,
∴铁环从A点滚动至F点其圆心所经过的路线长度l=4×5+2×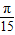 -4×
-4×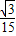 =(20+
=(20+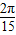 -
-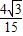 )米.
)米.
故答案为:(20+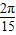 -
-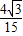 )米.
)米.
点评:此题考查了切线的性质,切线长定理,锐角三角函数定义,平行线的性质,以及弧长公式,利用了数形结合的思想,其中根据题意画出铁环从A点滚动至F点其圆心所经过的路线是解本题的关键.
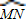 长-4HB,根据切线长定理及锐角三角函数定义,由GH的长,求出HB的长,由CD与BE平行,根据两直线平行同旁内角互补求出∠BCD的度数,进而求出∠MCN的度数,再由半径MC,利用弧长公式求出
长-4HB,根据切线长定理及锐角三角函数定义,由GH的长,求出HB的长,由CD与BE平行,根据两直线平行同旁内角互补求出∠BCD的度数,进而求出∠MCN的度数,再由半径MC,利用弧长公式求出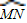 的长,代入表示出的路线中,即可求出铁环从A点滚动至F点其圆心所经过的路线长.
的长,代入表示出的路线中,即可求出铁环从A点滚动至F点其圆心所经过的路线长.解答:解:根据题意画出圆心运动的轨迹,如图所示:

∵Rt△GHB中,GH=0.2米,∠GBH=∠GBI=
 ∠HBI=60°,
∠HBI=60°,∴tan60°=
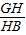 ,即HB=
,即HB=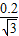 =
=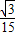 ,
,∵CD∥BE,∠CBE=60°,
∴∠BCD=120°,
∴∠MCN=60°,又CM=0.2米,
∴
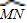 的长为
的长为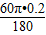 =
=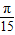 ,
,∵圆的半径为20厘米=0.2米,CD=EF=AB=BC=4m,
∴铁环从A点滚动至F点其圆心所经过的路线长度l=4×5+2×
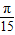 -4×
-4×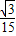 =(20+
=(20+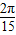 -
-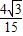 )米.
)米.故答案为:(20+
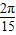 -
-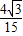 )米.
)米.点评:此题考查了切线的性质,切线长定理,锐角三角函数定义,平行线的性质,以及弧长公式,利用了数形结合的思想,其中根据题意画出铁环从A点滚动至F点其圆心所经过的路线是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目