题目内容
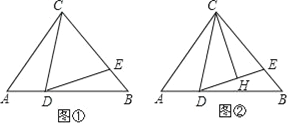
【题目】如图在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.
(1)如图①,若BC=BD,求证:CD=DE;
(2)如图②,过点C作CH⊥DE,垂足为H,若CD=BD,EH=1,求DE﹣BE的值.
【答案】(1)证明见解析(2)2
【解析】试题分析:(1)先根据条件得出∠ACD=∠BDE,BD=AC,再根据ASA判定△ADC≌△BED,即可得到CD=DE;(2)先根据条件得出∠DCB=∠CDE,进而得到CE=DE,再在DE上取点F,使得FD=BE,进而判定△CDF≌△DBE(SAS),得出CF=DE=CE,再根据CH⊥EF,运用三线合一即可得到FH=HE,最后得出DE﹣BE=DE﹣DF=EF=2HE=2.
试题解析:(1)∵AC=BC,∠CDE=∠A,
∴∠A=∠B=∠CDE,
∴∠ACD=∠BDE,
又∵BC=BD,
∴BD=AC,
在△ADC和△BED中,
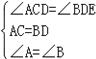 ,
,
∴△ADC≌△BED(ASA),
∴CD=DE;
(2)∵CD=BD,
∴∠B=∠DCB,
又∵∠CDE=∠B,
∴∠DCB=∠CDE,
∴CE=DE,
如图,在DE上取点F,使得FD=BE,
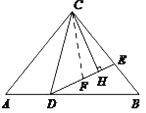
在△CDF和△DBE中,
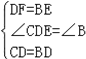 ,
,
∴△CDF≌△DBE(SAS),
∴CF=DE=CE,
又∵CH⊥EF,
∴FH=HE,
∴DE﹣BE=DE﹣DF=EF=2HE=2.

【题目】春天来了,小颖要用总长为12米的篱笆围一个长方形花圃,其一边靠墙(墙长9米),另外三边是篱笆,其中BC不超过9米.设垂直于墙的两边AB,CD的长均为x米,长方形花圃的面积为y米2 . 
(1)用x表示花圃的一边BC的长,判断x=1是否符合题意,并说明理由;
(2)求y与x之间的关系式;
根据关系式补充表格:
x(米) | … | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | … |
y(米2) | … | 13.5 | 16 | 17.5 | 17.5 | 13.5 | … |
观察表中数据,写出y随x变化的一个特征: .