题目内容
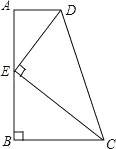
【题目】如图，在四边形ABCD中，AD∥BC，∠ABC=90°，E是AB上一点，且DE⊥CE．若AD=1，BC=2，CD=3，则CE与DE的数量关系正确的是（ ）
A．CE=
DE B．CE=
DE C．CE=3DE D．CE=2DE
【答案】B．
【解析】
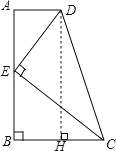
试题分析：过点D作DH⊥BC，利用勾股定理可得AB的长，利用相似三角形的判定定理可得△ADE∽△BEC，设BE=x，由相似三角形的性质可解得x，易得CE，DE 的关系．
过点D作DH⊥BC，由AD=1，BC=2，可求得CH=1，根据勾股定理可得DH=AB==2
，
因AD∥BC，∠ABC=90°，可得∠A=90°，即可得∠AED+∠ADE=90°，再由DE⊥CE，可得∠AED+∠BEC=90°，所以∠ADE=∠BEC，即可判定△ADE∽△BEC，由相似三角形的性质可得
，设BE=x，则AE=2
，即
，解得x=
，
，即CE=
，故答案选B．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
