题目内容
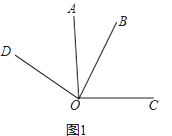
【题目】如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.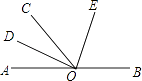
(1)若∠AOC=50°,求出∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
【答案】
(1)解:因为∠AOC=50°,OD平分∠AOC,
所以∠DOC= ![]() ∠AOC=25°,∠BOC=180°﹣∠AOC=130°,
∠AOC=25°,∠BOC=180°﹣∠AOC=130°,
所以∠BOD=∠DOC+∠BOC=155°;
(2)解:OE平分∠BOC.理由如下:
∵OD平分∠AOC,
∴∠DOA=∠DOC,
∵∠DOE=90°,
∴∠DOC+∠COE=90°,∠DOA+∠BOE=90°,
∴∠COE=∠BOE,
∴OE平分∠BOC.
【解析】(1)根据角平分线的定义知∠DOC的度数,然后根据邻补角的定义得出∠BOC的度数,然后根据∠BOD=∠DOC+∠BOC算出答案;
(2)根据角平分线的定义得出∠DOA=∠DOC,再根据等角的余角相等得出答案。
【考点精析】本题主要考查了角的平分线判定和余角和补角的特征的相关知识点,需要掌握可以证明三角形内存在一个点,它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点);互余、互补是指两个角的数量关系,与两个角的位置无关才能正确解答此题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目