题目内容
【题目】如图,折叠形ABCD的一边AD,点D落在BC边上的点F处,AE是折痕,已知AB=8cm,BC=10cm.则CE=__cm.
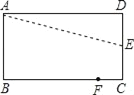
【答案】3
【解析】分析:首先根据折叠可得AF=AD=BC=10,在Rt△ABF中利用勾股定理计算出BF的长,进而得到FC的长,再设CE=xcm,则DE=EF=(8x)cm,在Rt△ECF中利用勾股定理列方程求解即可.
详解:连接AF,EF,
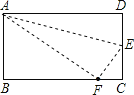
设CE=xcm,DE=EF=(8x)cm,
由折叠得,AF=AD=BC=10cm.
在Rt△ABF中,根据勾股定理可得:
![]() cm;
cm;
∴CF=BC-BF=10-6=4cm.
在Rt△ECF中,
∵CE2+CF2=EF2,
∴x2+42=(8-x)2,
解可得x=3,
故CE=3cm.
故答案为:3.

练习册系列答案
相关题目