题目内容
(2002•兰州)如图,已知两个等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过O2,则∠O1AB= 度.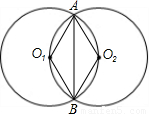
【答案】分析:连接O1O2,可得△BO2O1是等边三角形,再根据圆周角定理即可解答.
解答: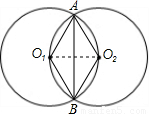 解:连接O1O2,
解:连接O1O2,
∵⊙O1和⊙O2是等圆,
∴O1B=O1O2=O2B,
∴△BO2O1是等边三角形,
∴∠BO2O1=60°,
∴∠O1AB= ∠BO2O1=30°(圆周角定理).
∠BO2O1=30°(圆周角定理).
故答案为:30.
点评:此题用到了等边三角形的判定和圆周角定理.
解答:
 解:连接O1O2,
解:连接O1O2,∵⊙O1和⊙O2是等圆,
∴O1B=O1O2=O2B,
∴△BO2O1是等边三角形,
∴∠BO2O1=60°,
∴∠O1AB=
 ∠BO2O1=30°(圆周角定理).
∠BO2O1=30°(圆周角定理).故答案为:30.
点评:此题用到了等边三角形的判定和圆周角定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,tanβ=
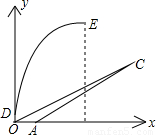
,tanβ= ,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).
,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).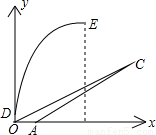
 ,tanβ=
,tanβ= ,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).
,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).