题目内容
(2002•兰州)如图在△ABC中∠A=70°,⊙O截△ABC的三条边所得的弦长相等,则∠BOC=( )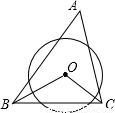
A.140°
B.135°
C.130°
D.125°
【答案】分析:先利用⊙O截△ABC的三条边所得的弦长相等,得出即O是△ABC的内心,从而,∠1=∠2,∠3=∠4,进一步求出∠BOC的度数.
解答: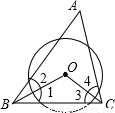 解:∵△ABC中∠A=70°,⊙O截△ABC的三条边所得的弦长相等,
解:∵△ABC中∠A=70°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3= (180°-∠A)=
(180°-∠A)= (180°-70°)=55°,
(180°-70°)=55°,
∴∠BOC=180°-(∠1+∠3)=180°-55°=125°.
故选D.
点评:本题考查的是三角形的内心,及三角形内角和定理,比较简单.
解答:
 解:∵△ABC中∠A=70°,⊙O截△ABC的三条边所得的弦长相等,
解:∵△ABC中∠A=70°,⊙O截△ABC的三条边所得的弦长相等,∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=
 (180°-∠A)=
(180°-∠A)= (180°-70°)=55°,
(180°-70°)=55°,∴∠BOC=180°-(∠1+∠3)=180°-55°=125°.
故选D.
点评:本题考查的是三角形的内心,及三角形内角和定理,比较简单.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 ,tanβ=
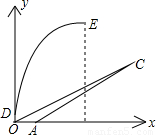
,tanβ= ,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).
,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).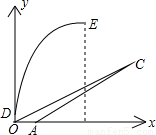
 ,tanβ=
,tanβ= ,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).
,位于点O正上方2米处的D点发射装置,可以向目标C发射一个火球点燃火炬,该火球运行的轨迹为一抛物线,当火球运行到距地面最大高度20米时,相应的水平距离为12米(图中E点).