Question

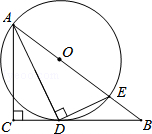
如图，在△ABO中，OA=OB，C是边AB的中点，以O为圆心的圆过点C，且与OA交于点E，与OB交于点F，连接CE，CF．

（1）求证：AB与⊙O相切．
（2）若∠AOB=∠ECF，试判断四边形OECF的形状，并说明理由．

Answer 1

解：（1）证明：连接OC，

∵在△ABO中，OA=OB，C是边AB的中点，
∴OC⊥AB。
∵OC为半径，
∴AB与⊙O相切。
（2）四边形OECF的形状是菱形，理由如下：
如图，取圆周角∠M，则∠M+∠ECF=180°。

由圆周角定理得：∠EOF=2∠M，
∵∠ECF=∠EOF，∴∠ECF=2∠M，
∴3∠M=180°，∠M=60°。
∴∠EOF=∠ECF=120°。
∵OA=OB，∴∠A=∠B=30°。
∴∠EOC=90°﹣30°=60°。
∵OE=OC，∴△OEC是等边三角形。∴EC=OE。
同理OF=FC。
∴OE=EC=FC=OF。∴四边形OECF是菱形。

试题分析：（1）连接OC，根据三线合一得出OC⊥AB，根据切线判定推出即可。
（2）取圆周角∠M，根据圆周角定理和圆内接四边形性质得出∠M+∠ECF=180°，∠EOF=2∠M，推出∠ECF=2∠M，求出∠M，求出∠EOF，得出等边三角形OEC，推出OE=EC，同理得出OF=FC，推出OE=OF=FC=EC，根据菱形判定推出即可。