题目内容
如图,A、B表示两个村庄,直线X表示高速公路,已知AB=50km,A、B到直线X的距离分别为10km和40km,要在高速公路旁修建一出口P.小民设计了两种方案,图(1)是方案一的示意图(AP与直线X垂直,垂足为P),P到A、B的距离之和S1=PA+PB; 图(2)是方案二的示意图(点A关于直线X的对称点是A',连接BA'交直线X于点P),P到A、B的距离之和S2=PA+PB.

(1)求S1 、S2 ,并比较它们的大小.
(2)请你说明S2=PA+PB的值为最小.
(3)拟建的另一高速公路Y与高速公路X垂直,建立如图所示的直角坐标系,B到直线Y的距离为30km,请你在X旁和Y旁各修建一出口P、Q,使P、A、B、Q 组成的四边形的周长最小.并求出这个最小值.

(1)求S1 、S2 ,并比较它们的大小.
(2)请你说明S2=PA+PB的值为最小.
(3)拟建的另一高速公路Y与高速公路X垂直,建立如图所示的直角坐标系,B到直线Y的距离为30km,请你在X旁和Y旁各修建一出口P、Q,使P、A、B、Q 组成的四边形的周长最小.并求出这个最小值.
(1)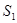 ﹥
﹥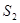 (2) S2=BA'为最小(3) 四边形的周长为
(2) S2=BA'为最小(3) 四边形的周长为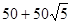
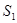 ﹥
﹥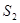 (2) S2=BA'为最小(3) 四边形的周长为
(2) S2=BA'为最小(3) 四边形的周长为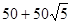
试题分析:解:⑴图10(1)中过B作BC⊥AP,垂足为C,则PC=40,又AP="10,"
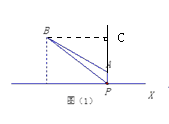
∴AC=30
在Rt△ABC 中,AB="50" AC=30 ∴BC=40
∴ BP=
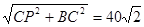
S1=
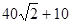
图10(2)中,过B作BC⊥AA′垂足为C,则A′C=50,
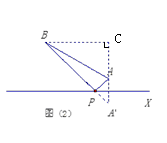
又BC=40
∴BA'=
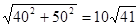
由轴对称知:PA=PA'
∴S2=BA'=
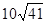
∴
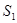 ﹥
﹥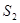
(2)如 图10(2),在公路上任找一点M,连接MA,MB,MA',由轴对称知MA=MA'
∴MB+MA=MB+MA'﹥A'B
∴S2=BA'为最小
(3)过A作关于X轴的对称点A', 过B作关于Y轴的对称点B',
连接A'B',交X轴于点P, 交Y轴于点Q,则P,Q即为所求
过A'、 B'分别作X轴、Y轴的平行线交于点G,
A'B'=
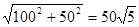
∴所求四边形的周长为
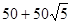
点评:本题难度中等,主要考查学生学习了三角形即多边形等几何知识后综合运用能力。作辅助线分析是这类题型的解题关键。注意数形结合思想的培养,运用到考试中。

练习册系列答案
相关题目


 最小。 (2分)
最小。 (2分) 绕点
绕点 逆时针旋转30°到正方形
逆时针旋转30°到正方形 ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )






 可以由△ABC绕点 A顺时针旋转900得到(点B1与点B是对应点,点C1与点C是对应点),连接CC’,则∠CC’B’的度数是( )。
可以由△ABC绕点 A顺时针旋转900得到(点B1与点B是对应点,点C1与点C是对应点),连接CC’,则∠CC’B’的度数是( )。
 的边长为4cm,则图中阴影部分的面积为( )cm2.
的边长为4cm,则图中阴影部分的面积为( )cm2.
 处,且点
处,且点