题目内容
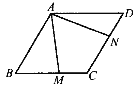
【题目】如图所示,在![]() ABCD中,∠ABC=60°,且AB=BC,∠MAN=60°.请探索BM,DN与AB的数量关系,并证明你的结论.
ABCD中,∠ABC=60°,且AB=BC,∠MAN=60°.请探索BM,DN与AB的数量关系,并证明你的结论.
【答案】BM+DN=AB
【解析】
试题分析:连结AC,先由证∠ABC=60°,AB=BC,证得△ABC为等边三角形,再结合平行四边形的性质即可得到△ABM≌△CAN,从而得到BM=CN,即可得到结果。
如图,连结AC,
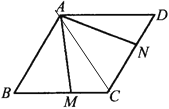
∵![]() ABCD,∠ABC=60°,
ABCD,∠ABC=60°,
∴AB=CD,∠BAD=120°,AB∥CD,
∵∠MAN=60°,
∴∠MAC+∠NAC =60°,
∵∠ABC=60°,AB=BC,
∴△ABC为等边三角形,
∴∠BAC=∠BCA=60°,AB=BC=AC,
∴∠BAM+∠NAC =60°,
∴∠BAM=∠NAC,
∵AB∥CD,
∴∠BAC=∠DCA=60°,
∵∠BAM=∠NAC,AB=AC,∠ABC=∠DCA=60°,
∴△ABM≌△CAN,
∴BM=CN,
∵AB=CD,
∴BM+DN= CN+DN=CD=AB.

练习册系列答案
相关题目