Question

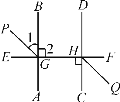
【题目】如图，AB⊥EF于点G，CD⊥EF于点H，GP平分∠EGB，HQ平分∠CHF，图中有哪些平行线？并说明理由．

Answer 1

【答案】AB∥CD，GP∥HQ.理由见解析

【解析】

根据垂直的性质,在同一平面内,垂直于同一条直线的两条直线平行, 因为AB⊥EF,CD⊥EF,所以AB∥CD ,再根据角平分线的定义可得: ∠1＝∠EGB＝45°,所以∠PGH＝∠1＋∠2＝135°,同理可得∠GHQ＝135°,根据内错角相等,两直线平行可得: GP∥HQ.

AB∥CD,GP∥HQ.理由如下:因为AB⊥EF,CD⊥EF,

所以AB∥CD(在同一平面内,垂直于同一条直线的两条直线平行),

因为AB⊥EF(已知),

所以∠EGB＝∠2＝90°(垂直定义)．

因为GP平分∠EGB(已知),

所以∠1＝∠EGB＝45°(角平分线的定义),

所以∠PGH＝∠1＋∠2＝135°,

同理可得∠GHQ＝135°,

所以∠PGH＝∠GHQ,所以GP∥HQ(内错角相等,两直线平行).