题目内容
【题目】如图,在平面直角坐标系中,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=1,tan∠ACB=2,将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF.点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,抛物线y=ax2+bx+2的图象过点A,C,F.
(1)求抛物线所对应函数的表达式;
(2)在边DE上是否存在一点M,使得以O,D,M为顶点的三角形与△ODE相似,若存在,求出经过M点的反比例函数的表达式,若不存在,请说明理由;
(3)在x轴的上方是否存在点P,Q,使以O,F,P,Q为顶点的平行四边形的面积是矩形OABC面积的2倍,且点P在抛物线上,若存在,请求出P,Q两点的坐标;若不能存在,请说明理由;
(4)在抛物线的对称轴上是否存在一点H,使得HA﹣HC的值最大,若存在,直接写出点H的坐标;若不存在,请说明理由.
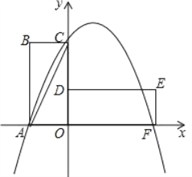
【答案】(1)y=﹣x2+x+2;(2)存在,y=0.5x-1;(3)存在,当点P为P1(0,1)时,点Q为Q1(2,2),Q2(﹣2,2);当点P为P2(1,2)时,点Q为Q3(3,2),Q4(﹣1,2);(4)存在,H(0.5,3)
【解析】解:(1)∵矩形OABC,∴BC=OA=1,OC=AB,∠B=90°,
∵tan∠ACB=2,∴AB:BC=2∴OC:OA=2,则OC=2,
∵将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF,
∴OF=2,则有A(﹣1,0)C(0,2)F(2,0)
∵抛物线y=ax2+bx+2的图象过点A,C,F,把点A、C、F坐标代入
得a-b+c=0,4a+2b+c=0,c=2∴解得a=-1,b=1,c=2∴函数表达式为y=﹣x2+x+2,
(2)存在,当∠DOM=∠DEO时,△DOM∽△DEO∴此时有DM:DO=DO:DE.
∴DM2=0.5,∴点M坐标为(0.5,1),
设经过点M的反比例函数表达式为y=kx-1,把点M代入解得k=0.5
∴经过M点的反比例函数的表达式为y=0.5x-1,
(3)存在符合条件的点P,Q.
∵S矩形ABCD=2×1=2,∴以O,F,P,Q为顶点平行四边形的面积为4,
∵OF=2,∴以O,F,P,Q为顶点平行四边形的高为2,
∵点P在抛物线上,设点P坐标为(m,2),∴﹣m2+m+2=2,解得m1=0,m2=1,
∴点P坐标为P1(0,2),P2(1,2)
∵以O,F,P,Q为顶点的四边形为平行四边形,∴PQ∥OF,PQ=OF=2.
∴当点P坐标为P1(0,1)时,点Q的坐标分别为Q1(2,2),Q2(﹣2,2);
当点P坐标为P2(1,2)时,点Q的坐标分别为Q3(3,2),Q4(﹣1,2);
(4)若使得HA﹣HC的值最大,则此时点A、C、H应在同一直线上,
设直线AC的函数解析式为y=kx+b,把点A(﹣1,0),点C(0,2)代入得
-k+b=0,b=2解得k=2,b=2∴直线AC的函数解析式为y=2x+2,
∵抛物线函数表达式为y=﹣x2+x+2,∴对称轴为x=0.5
∴把x=0.5代入y=2x+2 解得y=3∴点H的坐标为(0.5,3)