题目内容
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 的切线,连接
的切线,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交于点
交于点![]()
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]()
①求![]() 的长;
的长;
②连接![]() 交
交![]() 于
于![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)①12,②![]()
【解析】
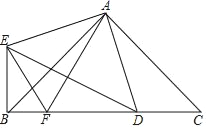
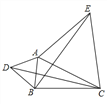
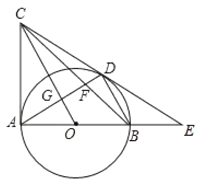
(1)连接OD,由切线的性质和圆周角定理可得∠CAB=90°=∠ADB,由“SAS”判定△CDO≌△CAO,则∠CDO=∠CAO=90°,然后根据切线的判定定理可得到CD是⊙O的切线;
(2)①设⊙O半径为r,则OD=OB=r,在Rt△ODE中利用勾股定理得到r2+42=(r+2)2,解得r=6,即OB=6,然后根据平行线分线段成比例定理,由DB∥OC得到DE:CD=BE:OB,于是可计算出CD=12;
②由△CDO≌△CAO得到AC=CD=6,在Rt△AOC中利用勾股定理计算出OC=![]() ,再证明Rt△OAG∽△OCA,利用相似比计算出OG=
,再证明Rt△OAG∽△OCA,利用相似比计算出OG=![]() ,则CG=OC-OG=
,则CG=OC-OG=![]() ,易得BD=2OG=
,易得BD=2OG=![]() ,然后利用CG∥BD得到
,然后利用CG∥BD得到![]() .
.
证明:![]() 如图,连接
如图,连接![]()
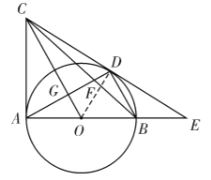
![]() 为
为![]() 的切线,
的切线,![]() 为
为![]() 的直径
的直径
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,且
,且![]()
![]() ,
,
![]() ,
,
![]() ,且
,且![]() 是半径,
是半径,
![]() 是
是![]() 的切线;
的切线;
![]() ①设
①设![]() 半径为
半径为![]() ,则
,则![]()
在![]() 中,
中,![]()
![]() ,解得
,解得![]()
![]() ,
,
![]()
![]()
![]()
②由(1)得△CDO≌△CAO,
∴AC=CD=12,
在Rt△AOC中,OC=![]() ,
,
∵∠AOG=∠COA,
∴Rt△OAG∽△OCA,
∴![]() ,
,
即![]() ,
,
∴OG=![]() ,
,
∴CG=OC-OG=![]() ,
,
∵OG∥BD,OA=OB,
∴OG为△ABD的中位线,
∴BD=2OG=![]() ,
,
∵CG∥BD,
∴![]()
∴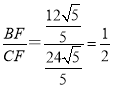

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目