题目内容
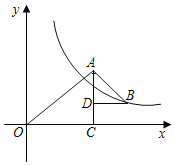
【题目】如图，△OAC和△BAD都是等腰直角三角形，∠ACO＝∠ADB＝90°，OC边在x轴上点A、D、C共线，反比例函数y＝
在第一象限的图象经过点B，则△OAC和△BAD的面积之差为_____（用含k的代数式表示）．
【答案】
k
【解析】
设△OAC和△BAD的直角边长分别为a、b，结合等腰直角三角形的性质及图象可得出点B的坐标，根据三角形的面积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论．
设△OAC和△BAD的直角边长分别为a、b，
则点B的坐标为（a+b，a﹣b）．
∵点B在反比例函数y＝
的第一象限图象上，
∴（a+b）×（a﹣b）＝a2﹣b2＝k．
∴S△OAC﹣S△BAD＝a2﹣b2＝（a2﹣b2）＝k．
故答案为k．
练习册系列答案
相关题目
【题目】某校八年级根据学生的学习成绩、学习能力将学生依次分为A、B、C三个层次，第一次月考后，选取了其中一个A层次班级的考试成绩分布情况进行处理分析，制成频数分布表（成绩得分均为整数）：
组别 | 成绩分组 | 频数 | 频率 |
1 | 39.5﹣49.5 | 2 | 0.05 |
2 | 49.5﹣59.5 | 4 | 0.10 |
3 | 59.5～69.5 | a | 0.20 |
4 | 69.5～79.5 | 10 | 0.25 |
5 | 79.5﹣89.5 | b | c |
6 | 89.5﹣100 | 6 | 0.15 |
合计 | 40 | 1.00 |
根据表中提供的信息解答下列各题：
（1）频数分布表中的a＝ ，b＝ ，c＝ ；
（2）将频数分布直方图补充完整；
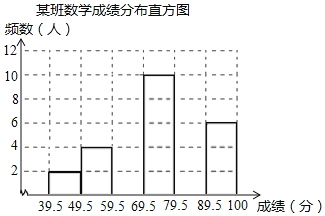
（3）小明正好在所选取的班级中，他认为：学校八年级共有20个班（平均每班40人），根据本班的成绩分布情况可知，在这次考试中，全年级90分以上为优秀，则优秀的人数约为 人，60分及以上为及格，及格的人数约为 人，及格的百分比约为 ；
（4）小明得到的数据会与实际情况相符吗？为什么？
