题目内容
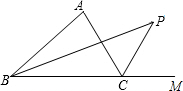
在△ABC中,∠B=90°,∠A、∠C的内角平分线交于点I,∠A、∠C的外角平分线交于点D,则∠AIC=______,∠ADC=______.
如图所示:
∵∠B=90°,∠A、∠C的内角平分线交于点I,
∴∠BAI=∠CAI,∠ACI=∠ICB,
∴∠BAC+∠ACB=90°,
∴
(∠BAC+∠ACB)=45°,
∴∠AIC=180°-45°=135°,
∵∠A、∠C的外角平分线交于点D,
∴∠MAD=∠DAC,∠DCA=∠DCN,
又∵∠MAC+∠ACN=360°-(∠BAC+∠BCA)=270°,
∴
(∠MAC+∠ACN)=135°,
∴∠ADC=180°-135°=45°.
故答案为:135°,45°.
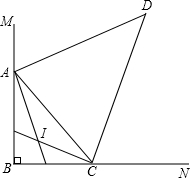
∵∠B=90°,∠A、∠C的内角平分线交于点I,
∴∠BAI=∠CAI,∠ACI=∠ICB,
∴∠BAC+∠ACB=90°,
∴
| 1 |
| 2 |
∴∠AIC=180°-45°=135°,
∵∠A、∠C的外角平分线交于点D,
∴∠MAD=∠DAC,∠DCA=∠DCN,
又∵∠MAC+∠ACN=360°-(∠BAC+∠BCA)=270°,
∴
| 1 |
| 2 |
∴∠ADC=180°-135°=45°.
故答案为:135°,45°.


练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目