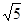题目内容
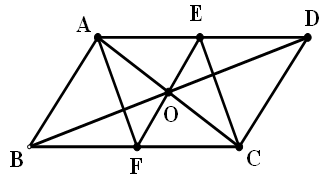
如图:在□ABCD中,对角线 与BD交于点O,过点O的直线EF分别与AD、BC交于点E、F, EF⊥AC,连结AF、CE.
与BD交于点O,过点O的直线EF分别与AD、BC交于点E、F, EF⊥AC,连结AF、CE.
(1)求证:OE=OF
(2)请判断四边形AECF是什么特殊四边形,请证明你的结论;
(3)若∠EAF=60°,AE=6,求四边形AECF的面积.
 与BD交于点O,过点O的直线EF分别与AD、BC交于点E、F, EF⊥AC,连结AF、CE.
与BD交于点O,过点O的直线EF分别与AD、BC交于点E、F, EF⊥AC,连结AF、CE. 
(1)求证:OE=OF
(2)请判断四边形AECF是什么特殊四边形,请证明你的结论;
(3)若∠EAF=60°,AE=6,求四边形AECF的面积.
(1)见解析(2)菱形,证明见解析(3)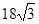
(1)证明:在□ABCD中,对角线 与BD交于点O,得
与BD交于点O,得
AE∥CF, OA=OC,∠AOE=∠COF,
∴∠OAE=∠OCF
∴△AOE≌△COF (ASA)
∴ OE=OF--------------3分
(2)四边形AECF是菱形。理由如下:
∵OE=OF,OA=OC
∴四边形AECF是平行四边形。(对角线互相平分的四边形是平行四边形)
又 ∵EF⊥AC
∴□。(对角线互相垂直的平行四边形是菱形)-----3分
(3)在菱形AECF中,EF⊥AC,∠EAF=60°,AE=6
∴ ∠EAC=30°(菱形的对角线平分每组对角) ,∠AOE=90°
∴ OE=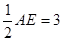 (直角三角形中,30°角所对的直角边等于斜边的一半)
(直角三角形中,30°角所对的直角边等于斜边的一半)
在Rt△AOE中,由勾股定理,得AO=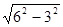 =
=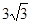 ----2分
----2分
∴EF=2OE=6,AC=2AO=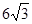
菱形AECF=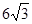
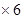
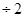 =
=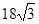 ----2分
----2分
(1)在平行四边形,可得一组内错角,一组对顶角分别相等,又有一边相等,则证明△AOE≌△COF即可.
(2)证明AECF是平行四边形,然后于EF⊥AC得出AECF是菱形;
(3)先求出AE、AO的长,从而得出EF、AC的长,最后求出菱形AECF的面积。
 与BD交于点O,得
与BD交于点O,得AE∥CF, OA=OC,∠AOE=∠COF,
∴∠OAE=∠OCF
∴△AOE≌△COF (ASA)
∴ OE=OF--------------3分
(2)四边形AECF是菱形。理由如下:
∵OE=OF,OA=OC
∴四边形AECF是平行四边形。(对角线互相平分的四边形是平行四边形)
又 ∵EF⊥AC
∴□。(对角线互相垂直的平行四边形是菱形)-----3分
(3)在菱形AECF中,EF⊥AC,∠EAF=60°,AE=6
∴ ∠EAC=30°(菱形的对角线平分每组对角) ,∠AOE=90°
∴ OE=
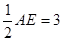 (直角三角形中,30°角所对的直角边等于斜边的一半)
(直角三角形中,30°角所对的直角边等于斜边的一半) 在Rt△AOE中,由勾股定理,得AO=
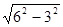 =
=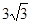 ----2分
----2分∴EF=2OE=6,AC=2AO=
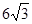
菱形AECF=
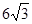
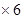
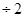 =
=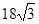 ----2分
----2分(1)在平行四边形,可得一组内错角,一组对顶角分别相等,又有一边相等,则证明△AOE≌△COF即可.
(2)证明AECF是平行四边形,然后于EF⊥AC得出AECF是菱形;
(3)先求出AE、AO的长,从而得出EF、AC的长,最后求出菱形AECF的面积。

练习册系列答案
相关题目
 ABCD中,E,F分别是BC、AD上的点,且BE=DF.求证:AE=CF.
ABCD中,E,F分别是BC、AD上的点,且BE=DF.求证:AE=CF.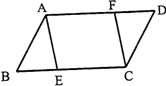
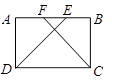
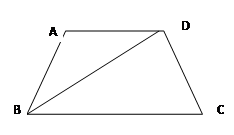
 方格中,每个小正方形的边长都是
方格中,每个小正方形的边长都是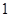 ,按下列要求画格点梯形(顶点都在格点上的梯形)并直接写出所画梯形的周长.
,按下列要求画格点梯形(顶点都在格点上的梯形)并直接写出所画梯形的周长.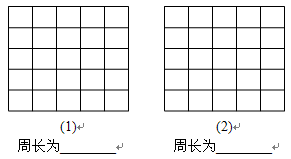
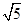 的梯形;
的梯形;