题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
【答案】
(1)解:补全图形,如图所示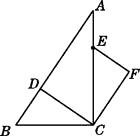
(2)证明:由旋转的性质得:∠DCF=90°,DC=FC,BC=EC,∴∠DCE+∠ECF=90°
∵∠ACB=90°,
∴∠DCE+∠BCD=90°.
∴∠ECF=∠BCD.
∵EF∥DC,
∴∠EFC+∠DCF=180°.
∴∠EFC=90°,
在△BDC和△EFC中,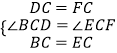
∴△BDC≌△EFC(SAS).
∴∠BDC=∠EFC=90°
【解析】(1)根据题意将线段CD绕点C按顺时针方向旋转90°,画出图形即可。
(2)根据旋转的性质得出∠DCF=90°,DC=FC,BC=EC,∠DCE+∠ECF=90°,再证明∠ECF=∠BCD,∠EFC=90°,然后证明△BDC≌△EFC,再根据全等三角形的性质即可证得结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下: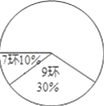
命中环数 | 10 | 9 | 8 | 7 |
命中次数 | 3 | 2 |
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.



