题目内容
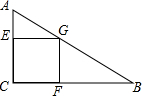 如图,在直角三角形ABC中,∠C是直角,G为AB上一点,过点G作GE、GF分别垂直于AC、BC,垂足分别为E、F,若四边形EGFC是正方形,AE=4,FB=9,求正方形EGFC的边长是________.
如图,在直角三角形ABC中,∠C是直角,G为AB上一点,过点G作GE、GF分别垂直于AC、BC,垂足分别为E、F,若四边形EGFC是正方形,AE=4,FB=9,求正方形EGFC的边长是________.
6
分析:正方形各边长相等,故DE=EF=BD=BF,根据DE与BC的比值和EF与AB的比值即可求得BD的值,即可解题.
解答:∵四边形EGFC是正方形,
∴EC=CF=FG=GE,且EG∥BC,GF∥AC.
∴△AEG∽△ABC,△BGF∽△BAC,
∴ =
=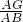 ,
, =
=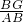 ,
,
又∵AG+GB=AB,
∴ +
+ =
=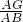 +
+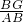 =
=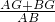 =1,
=1,
∵AE=4,FB=9,
∴ +
+ =
=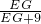 +
+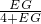 =1,
=1,
∴EG=6.即正方形EGFC的边长是6;
故答案是:6.
点评:本题考查了相似三角形的判定与性质、正方形的性质.解答此题还可以利用“平行线分线段成比例、勾股定理”进行解答.
分析:正方形各边长相等,故DE=EF=BD=BF,根据DE与BC的比值和EF与AB的比值即可求得BD的值,即可解题.
解答:∵四边形EGFC是正方形,
∴EC=CF=FG=GE,且EG∥BC,GF∥AC.
∴△AEG∽△ABC,△BGF∽△BAC,
∴
 =
=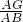 ,
, =
=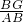 ,
,又∵AG+GB=AB,
∴
 +
+ =
=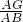 +
+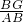 =
=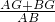 =1,
=1,∵AE=4,FB=9,
∴
 +
+ =
=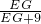 +
+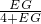 =1,
=1,∴EG=6.即正方形EGFC的边长是6;
故答案是:6.
点评:本题考查了相似三角形的判定与性质、正方形的性质.解答此题还可以利用“平行线分线段成比例、勾股定理”进行解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
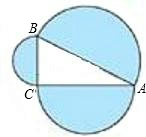 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.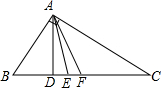 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,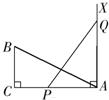 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=