题目内容
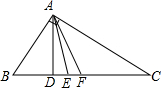 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,(1)证明:AF=BF=CF;
(2)写出∠FAE和∠DAE的关系并证明你的结论.
分析:(1)根据题意可知BF=CF,由AF为BC的中线,即可推出结论;
(2)由AD⊥BC,AF=BF=CF,可知,∠C=∠BAD=∠FAC,结合AE为角平分线,即可推出∠FAE=∠DAE.
(2)由AD⊥BC,AF=BF=CF,可知,∠C=∠BAD=∠FAC,结合AE为角平分线,即可推出∠FAE=∠DAE.
解答:(1)证明:∵直角三角形ABC中,AF为BC的中线,
∴BF=CF,AF=
BC,
∴AF=BF=CF,
(2)解:∵∠BAC=90°,AD⊥BC,
∴∠C=∠BAD,
∵AF=BF=CF,
∴∠C=∠BAD=∠FAC,
∵AE为角平分线,
∴∠BAE=∠EAC,
∴∠FAE=∠DAE.
∴BF=CF,AF=
| 1 |
| 2 |
∴AF=BF=CF,
(2)解:∵∠BAC=90°,AD⊥BC,
∴∠C=∠BAD,
∵AF=BF=CF,
∴∠C=∠BAD=∠FAC,
∵AE为角平分线,
∴∠BAE=∠EAC,
∴∠FAE=∠DAE.
点评:本题主要考查直角三角形斜边上的中线的性质,角平分线的性质、垂线的性质,关键在于根据题意证明AF=BF=CF,推出∠C=∠BAD=∠FAC.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
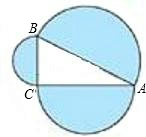 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.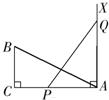 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=