题目内容
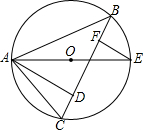如图，AE是△ABC外接圆O的直径，AD是△ABC的边BC上的高，EF⊥BC，F为垂足．（1）求证：BF=CD；
（2）若CD=1，AD=3，BD=6，求⊙O的直径．
分析：（1）过O作OM⊥BC于M，易得AD∥OM∥EF，由于AO=OE，根据平行线分线段成比例定理可得DM=FM；由垂径定理知：BM=CM，即可证得CD=BF．
（2）首先由勾股定理求得AB、AC的长，连接BE，通过相似三角形△ACD∽△AEB得到的比例线段，即可求得⊙O的直径．
（2）首先由勾股定理求得AB、AC的长，连接BE，通过相似三角形△ACD∽△AEB得到的比例线段，即可求得⊙O的直径．
解答：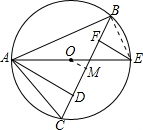
（1）证明：过O作OM⊥BC于M，则CM=BM；
∵AD⊥BC，EF⊥BC，OM⊥BC，
∴AD∥OM∥EF，
又∵OA=OE，
∴DM=MF，故CM-DM=BM-MF，即BF=CD．
（2）解：连接BE，则∠ABE=90°；
在Rt△ABD中，AD=3，BD=6，由勾股定理得：
AB=
=3
；
同理可求得：AC=
．
∵∠C=∠AEB，∠ADC=∠ABE=90°，
∴△ADC∽△ABE，
∴
=
，即
=
，解得AE=5
；
即⊙O的直径为5
．
（1）证明：过O作OM⊥BC于M，则CM=BM；∵AD⊥BC，EF⊥BC，OM⊥BC，
∴AD∥OM∥EF，
又∵OA=OE，
∴DM=MF，故CM-DM=BM-MF，即BF=CD．
（2）解：连接BE，则∠ABE=90°；
在Rt△ABD中，AD=3，BD=6，由勾股定理得：
AB=
| AD2+BD2 |
| 5 |
同理可求得：AC=
| 10 |
∵∠C=∠AEB，∠ADC=∠ABE=90°，
∴△ADC∽△ABE，
∴
| AD |
| AB |
| AC |
| AE |
| 3 | ||
3
|
| ||
| AE |
| 2 |
即⊙O的直径为5
| 2 |
点评：此题主要考查了三角形的外接圆、平行线分线段成比例定理、垂径定理、圆周角定理、勾股定理以及相似三角形的判定和性质，综合性强，难度适中．
练习册系列答案
相关题目
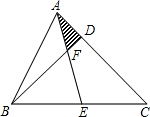如图，AE是△ABC的中线，F在AE上，AE=3AF，BF延长线交AC于点D．若△ABC的面积是48，求△AFD的面积．
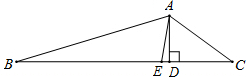（2012•梧州）如图，AE是△ABC的角平分线，AD⊥BC于点D，若∠BAC=128°，∠C=36°，则∠DAE的度数是（ ）
如图，AE是△ABC的中线，已知EC=6，DE=2，则BD的长为（ ）
如图，AE是△ABC的中线，A、E、D三点在一直线上，且AE=DE，那么△BDE可以看做是由