题目内容
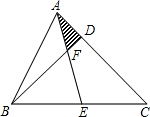 如图,AE是△ABC的中线,F在AE上,AE=3AF,BF延长线交AC于点D.若△ABC的面积是48,求△AFD的面积.
如图,AE是△ABC的中线,F在AE上,AE=3AF,BF延长线交AC于点D.若△ABC的面积是48,求△AFD的面积.
分析:过点E作EH∥BD,交AC于点H.由平行线得△ADF∽△AHE,且相似比为1:3.故求出△AHE的面积即可得解.根据三角形中位线定理得DH=HC.由AD:AH=AF:AE=1:3可得AD:DH:HC=1:2:2,即AH:AC=3:5.所以S△AHE:S△ACE=3:5.因为中线分三角形为面积相等的两个三角形,所以可求S△ACE=
S△ABC.
| 1 |
| 2 |
解答: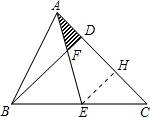 解:过点E作EH∥BD,交AC于点H.
解:过点E作EH∥BD,交AC于点H.
则△ADF∽△AHE.
∵AE=3AF,∴S△AHE=9S△ADF,即S△ADF=
S△AHE.
∵EH∥DF,∴AF:AE=AD:AH=1:3,
∴AD:DH=1:2.
又∵E是BC中点,∴H是CD中点,即DH=HC.
∴AH:AC=3:5.则S△AHE:S△ACE=3:5.
∵△ABC的面积是48,
∴△ACE的面积是24.
∴S△AHE=
,则S△ADF=
×
=
.
 解:过点E作EH∥BD,交AC于点H.
解:过点E作EH∥BD,交AC于点H.则△ADF∽△AHE.
∵AE=3AF,∴S△AHE=9S△ADF,即S△ADF=
| 1 |
| 9 |
∵EH∥DF,∴AF:AE=AD:AH=1:3,
∴AD:DH=1:2.
又∵E是BC中点,∴H是CD中点,即DH=HC.
∴AH:AC=3:5.则S△AHE:S△ACE=3:5.
∵△ABC的面积是48,
∴△ACE的面积是24.
∴S△AHE=
| 72 |
| 5 |
| 1 |
| 9 |
| 72 |
| 5 |
| 8 |
| 5 |
点评:此题考查相似三角形的判定与性质及面积计算,综合性很强,难度较大.

练习册系列答案
相关题目
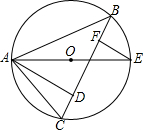 如图,AE是△ABC外接圆O的直径,AD是△ABC的边BC上的高,EF⊥BC,F为垂足.
如图,AE是△ABC外接圆O的直径,AD是△ABC的边BC上的高,EF⊥BC,F为垂足.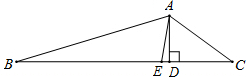 (2012•梧州)如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是( )
(2012•梧州)如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是( )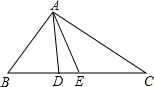 如图,AE是△ABC的中线,已知EC=6,DE=2,则BD的长为( )
如图,AE是△ABC的中线,已知EC=6,DE=2,则BD的长为( )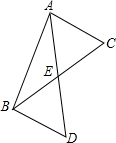 如图,AE是△ABC的中线,A、E、D三点在一直线上,且AE=DE,那么△BDE可以看做是由
如图,AE是△ABC的中线,A、E、D三点在一直线上,且AE=DE,那么△BDE可以看做是由