题目内容
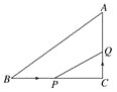
【题目】湖州西山漾湿地公园一休闲草坪上有一架秋千．秋千静止时，底端A到地面的距离AB为0.5m，从竖直位置开始，向右可摆动的最大夹角为37°，若秋千的长OA＝2m．（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）
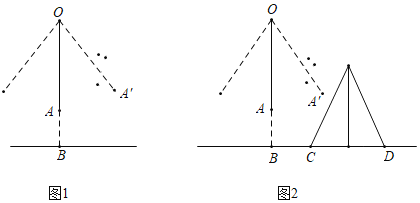
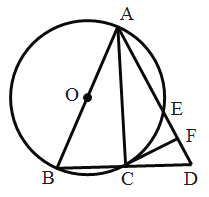
（1）如图1，当向右摆动到最大夹角时，求A'到地面的距离；
（2）如图2，若有人在B点右侧搭建了一个等腰三角形帐篷，已知BC＝0.6m，CD＝2m，帐篷的高为1.8m，当人站立在秋千上，请问摆动的过程中是否会撞到帐篷？若不会撞到，请说明理由；若会撞到，则帐篷应该向右移动超过多少米才能不被撞到？
【答案】（1）0.9m；（2）会撞到，帐篷应该向右移动超过0.1米才能不被撞到．
【解析】
（1）过A′作A′N⊥OA于C，解直角三角形即可得到结论；
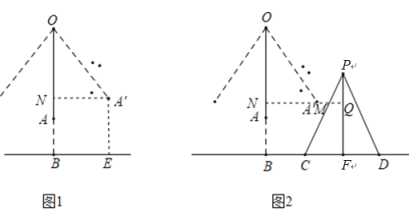
（2）将帐篷的示意图标注字母如图所示，延长NA′交PF于点Q,交PC于点M.当秋千摆动的夹角最大时，由（1）知，FQ＝NB＝0.9m，由△PMQ∽△PCF可知MQ＝0.5m，求得A′N＝1.2m，当A′恰好在帐篷的边CP时，NQ＝1.7m，BF＝1.6m，于是得到结论．
解：（1）过A′作A′N⊥OA于C，
在Rt△ONA′中，
∴ON＝OA′×cos37°≈0.8×OA′＝0.8×2＝1.6，
∴NB＝AN+AB＝2﹣1.6+0.5＝0.9，
∴A'到地面的距离为0.9m；
（2）将帐篷的示意图标注字母如图所示，延长NA′交PF于点Q,交PC于点M.
当秋千摆动的夹角最大时，由（1）知，FQ＝NB＝0.9m，
∵CF＝1， PF=1.8，∴PQ=0.9.
由△PMQ∽△PCF可知MQ＝0.5m，
由A′N＝A′O·sin37°≈2×0.6=1.2m，
当A′恰好在帐篷的边CP时，NQ＝1.7m，BF＝1.6m，
∵NQ＞BF，
∴会撞到，
∴移动的距离为1.7﹣1.6＝0.1m．
