题目内容
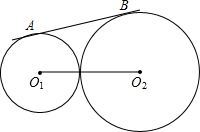 如图,圆O1与圆O2相外切,两圆半径分别为2和3,则两圆公切线AB长为( )
如图,圆O1与圆O2相外切,两圆半径分别为2和3,则两圆公切线AB长为( )A、2
| ||
B、
| ||
C、2
| ||
D、2
|
分析:作出辅助线,根据勾股定理可得.
解答: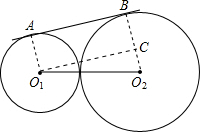 解:如图,作O1C⊥BO2,
解:如图,作O1C⊥BO2,
则O1O2=2+3=5,O2C=3-2=1,
根据勾股定理,AB=O1C=
=2
.
故选D.
 解:如图,作O1C⊥BO2,
解:如图,作O1C⊥BO2,则O1O2=2+3=5,O2C=3-2=1,
根据勾股定理,AB=O1C=
| 52-12 |
| 6 |
故选D.
点评:作出辅助线,根据勾股定理解答.

练习册系列答案
相关题目
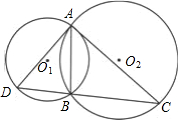 如图,圆O1与圆O2相交于A、B,过A作圆O1的切线交圆O2于C,连CB并延长交圆O1于D,连AD,AB=2,BD=3,BC=5,则AD的长为( )
如图,圆O1与圆O2相交于A、B,过A作圆O1的切线交圆O2于C,连CB并延长交圆O1于D,连AD,AB=2,BD=3,BC=5,则AD的长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
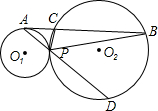 线AP交圆O2于点D,连接DC、PC.
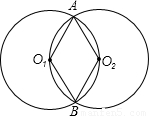
线AP交圆O2于点D,连接DC、PC.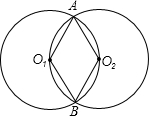 如图,圆O1与圆O2相交于A、B两点,它们的半径都为2,圆O1经过点O2,则四边形O1AO2B的面积为
如图,圆O1与圆O2相交于A、B两点,它们的半径都为2,圆O1经过点O2,则四边形O1AO2B的面积为