题目内容
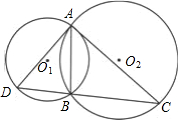 如图,圆O1与圆O2相交于A、B,过A作圆O1的切线交圆O2于C,连CB并延长交圆O1于D,连AD,AB=2,BD=3,BC=5,则AD的长为( )
如图,圆O1与圆O2相交于A、B,过A作圆O1的切线交圆O2于C,连CB并延长交圆O1于D,连AD,AB=2,BD=3,BC=5,则AD的长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
分析:首先根据切割线定理求得AC2的值,再根据勾股定理即可求得AD的长.
解答:解:∵AC是圆O2的切线,
∴∠CAB=∠D,
又∵∠C=∠C,
∴△ACD∽△BCA,
∴AC2=BC•CD,AB=2,BD=3,BC=5,
∴AC2=40,
∴AD=
=2
.
故选D.
∴∠CAB=∠D,
又∵∠C=∠C,
∴△ACD∽△BCA,
∴AC2=BC•CD,AB=2,BD=3,BC=5,
∴AC2=40,
∴AD=
| 64-40 |
| 6 |
故选D.
点评:此题综合运用了切割线定理、切线的性质定理以及勾股定理.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
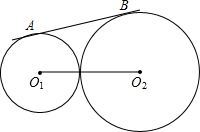 如图,圆O1与圆O2相外切,两圆半径分别为2和3,则两圆公切线AB长为( )
如图,圆O1与圆O2相外切,两圆半径分别为2和3,则两圆公切线AB长为( )A、2
| ||
B、
| ||
C、2
| ||
D、2
|
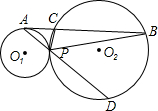 线AP交圆O2于点D,连接DC、PC.
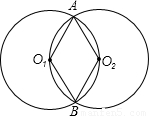
线AP交圆O2于点D,连接DC、PC.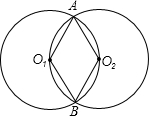 如图,圆O1与圆O2相交于A、B两点,它们的半径都为2,圆O1经过点O2,则四边形O1AO2B的面积为
如图,圆O1与圆O2相交于A、B两点,它们的半径都为2,圆O1经过点O2,则四边形O1AO2B的面积为