题目内容
填写适当的理由:如图,已知:AB∥ED,你能求出∠B+∠BCD+∠D的大小吗?
解:过点C画FC∥AB
∵AB∥ED( )
FC∥AB( )
∴FC∥ED( )
∴∠B+∠1=180°
∠D+∠2=180°( )
∴∠B+∠1+∠D+∠2= °( )
即:∠B+∠BCD+∠D=360°.
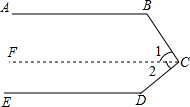
解:过点C画FC∥AB
∵AB∥ED( )
FC∥AB( )
∴FC∥ED( )
∴∠B+∠1=180°
∠D+∠2=180°( )
∴∠B+∠1+∠D+∠2= °( )
即:∠B+∠BCD+∠D=360°.

详见试题解析.
试题分析:首先过点C画FC∥AB,根据平行于同一直线的两直线平行,可得FC∥ED,然后由两直线平行,同旁内角互补,求得∠B+∠1=180°,∠D+∠2=180°,继而证得结论.
试题分析:首先过点C画FC∥AB,根据平行于同一直线的两直线平行,可得FC∥ED,然后由两直线平行,同旁内角互补,求得∠B+∠1=180°,∠D+∠2=180°,继而证得结论.
试题解析:过点C画FC∥AB,
∵AB∥ED(已知)
FC∥AB(作图)
∴FC∥ED(平行于同一直线的两直线平行)
∴∠B+∠1=180°
∠D+∠2=180°(两直线平行,同旁内角互补)
∴∠B+∠1+∠D+∠2=360°(等式的性质)
即:∠B+∠BCD+∠D=360°.
故答案为:已知;平行于同一直线的两直线平行;两直线平行,同旁内角互补;360.

练习册系列答案
相关题目

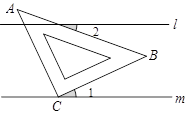
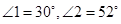 ,则
,则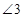 的度数等于( )
的度数等于( )
