题目内容
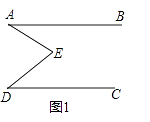
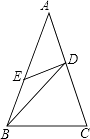
【题目】如图,已知射线CD∥OA,点E、点F是OA上的动点,CE平分∠OCF,且满足∠FCA=∠FAC.
(1)若∠O=∠ADC,判断AD与OB的位置关系,证明你的结论.
(2)若∠O=∠ADC=60°,求∠ACE的度数.
(3)在(2)的条件下左右平行移动AD,∠OEC和∠CAD存在怎样的数量关系?请直接写出结果(不需写证明过程)
【答案】
(1)解:∵CD∥OA,
∴∠BCD=∠O,
∵∠O=∠ADC,
∴∠BCD=∠CDA,
∴AD∥OB;
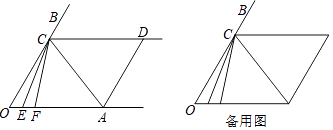
(2)解:∵∠O=∠ADC=60°,
∴∠BCD=60°,
∴∠OCD=120°,
∵CD∥OA,
∴∠DCA=∠CAO,
∵∠FCA=∠FAC,
∴∠DCA=FCA,
∵CE平分∠OCF,
∴∠OCE=∠FCE,
∴∠ECF+∠ACF= ![]() ∠OCD=60°,
∠OCD=60°,
∴∠ACE=60°;
(3)解:∠CAD+∠OEC=180°,
理由:∵AD∥OC,
∴∠CAD=∠OCA,
∵∠OCA=∠OCE+∠ACE=60°+∠OCE,
∵∠AEC=∠O+∠OCE=60°+∠OCE,
∴∠AEC=∠CAD,
∵∠AEC+∠OEC=180°,
∴∠CAD+∠OEC=180°.
【解析】(1)首先根据平行线的性质得到∠BCD=∠O,然后通过等量代换得到∠BCD=∠CDA,于是得到结论;
(2)首先依据邻补角的定义得到∠OCD=120°,然后再根据平行线的性质得到∠DCA=∠CAO,通过等量代换得到∠DCA=FCA,由角平分线的定义得到∠OCE=∠FCE,于是得到结论;
(3)首先根据平行线的性质得到∠CAD=∠OCA,然后可推出∠AEC=∠CAD,接下来,根据平角的定义得到∠AEC+∠OEC=180°,于是得到结论.
【考点精析】根据题目的已知条件,利用平行线的性质和平移的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案