Question

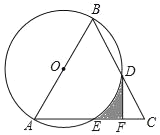
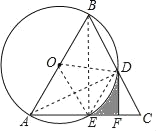
【题目】如图，在△ABC中，AB＝AC，以AB为直径作⊙O，分别交BC，AC于点D，E，过点D作DF⊥AC于点F

（1）求证：DF是⊙O的切线；

（2）若∠C＝60°，⊙O的半径为2，求由弧DE，线段DF，EF围成的阴影部分的面积（结果保留根号和π）

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）连接AD、OD，先利用等腰三角形的性质证CD=BD，再证OD为△ABC的中位线得DO∥AC，根据DF⊥AC可得；
（2）连接OE、BE，DE，根据已知条件得到△ABC是等边三角形，求得DE∥AB，于是得到S△ADE=S△ODE，根据阴影部分面积=S梯形EFDO-S扇形DOE计算可得．

解：（1）如图，连接AD、OD，

∵AB为⊙O的直径，

∴AD⊥BC，

∵AB＝AC，

∴BD＝CD，

∵OA＝OB，

∴OD∥AC，

∵DF⊥AC，

∴DF⊥OD，

∴DF是⊙O的切线；

（2）连接OE，BE，DE，

∵AB＝AC，∠C＝60°，

∴△ABC是等边三角形，

∵AB为⊙O的直径，

∴BE⊥AC，

∴AE＝CE，

∴DE∥AB，

∴S△ADE＝S△ODE，

∵⊙O的半径为2，∠BAD＝∠CAD＝30°，

∴AD＝2 ，

∴DF＝AD＝，AF＝3，

∵∠DOE＝2∠DAC＝60°，

∴阴影部分面积为S梯形EFDO﹣S扇形DOE

＝S三角形ADF﹣S扇形DOE＝××3﹣＝﹣ ．

故答案为（1）证明见解析；（2）．