题目内容
 如图,P是⊙O外一点,PA是⊙O的切线,A是切点,B是⊙O上一点,且PA=PB,延长BO分别与⊙O切线PA相交于点C、Q两点.
如图,P是⊙O外一点,PA是⊙O的切线,A是切点,B是⊙O上一点,且PA=PB,延长BO分别与⊙O切线PA相交于点C、Q两点.(1)求证:PB是⊙O的切线;
(2)D为PB的中点,QD交AB于点E,若⊙O的半径为3,CQ=2,求
| AE |
| BE |
考点:切线的判定与性质,相似三角形的判定与性质
专题:证明题
分析:(1)根据切线的性质由PA是⊙O的切线得到∠OAP=90°,再利用“SSS”判断△POA≌△POB,则∠OBP=∠OAP=90°,然后根据切线的判定定理即可得到结论;
(2)先用勾股定理计算出AQ=4,再计算出AP=6,利用切线长定理可得到H点为AB的中点,易得DH为△BAP的中位线,则DH=
PA=3,DH∥PA,利用DH∥AQ得到△DHE∽△QEA,所以
=
=
,设AE=4t,HE=3t,则AH=AE+HE=7t,于是BE=BH+HE=AH+HE=10t,最后计算
.
(2)先用勾股定理计算出AQ=4,再计算出AP=6,利用切线长定理可得到H点为AB的中点,易得DH为△BAP的中位线,则DH=
| 1 |
| 2 |
| AE |
| HE |
| AQ |
| DH |
| 4 |
| 3 |
| AE |
| BE |
解答:(1)证明:连结OA,如图,
∵PA是⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
在△POA和△POB中
,
∴△POA≌△POB(SSS),
∴∠OBP=∠OAP=90°,
∴OB⊥PB,
∴PB是⊙O的切线;
(2)AB与OP交于H,连结DH,如图,
在Rt△OCA中,OQ=OC+CQ=3+2=5,OA=3,则AQ=
=4,
设PA=x,则PB=x,PQ=4+x,
在Rt△PBQ中,∵BQ2+BP2=PQ2,
∴82+x2=(x+4)2,解得x=6,
∴PA=PB=6,
∵PA与PB为⊙O的切线,
∴OP平分∠BPA,
∴OP垂直平分AB,即点H为AB的中点,
∵D为PB的中点,
∴DH为△BAP的中位线,
∴DH=
PA=3,DH∥PA,
∵DH∥AQ,
∴△DHE∽△QEA,
∴
=
=
,
设AE=4t,HE=3t,则AH=AE+HE=7t,
∴BE=BH+HE=AH+HE=7t+3t=10t,
∴
=
=
.

∵PA是⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
在△POA和△POB中
|
∴△POA≌△POB(SSS),
∴∠OBP=∠OAP=90°,
∴OB⊥PB,
∴PB是⊙O的切线;
(2)AB与OP交于H,连结DH,如图,
在Rt△OCA中,OQ=OC+CQ=3+2=5,OA=3,则AQ=
| 52-32 |
设PA=x,则PB=x,PQ=4+x,
在Rt△PBQ中,∵BQ2+BP2=PQ2,
∴82+x2=(x+4)2,解得x=6,
∴PA=PB=6,
∵PA与PB为⊙O的切线,
∴OP平分∠BPA,
∴OP垂直平分AB,即点H为AB的中点,
∵D为PB的中点,
∴DH为△BAP的中位线,
∴DH=
| 1 |
| 2 |
∵DH∥AQ,
∴△DHE∽△QEA,
∴
| AE |
| HE |
| AQ |
| DH |
| 4 |
| 3 |
设AE=4t,HE=3t,则AH=AE+HE=7t,
∴BE=BH+HE=AH+HE=7t+3t=10t,
∴
| AE |
| BE |
| 4t |
| 10t |
| 2 |
| 5 |
点评:本题考查了切线的判定与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了勾股定理和相似三角形的判定与性质.

练习册系列答案
相关题目
下列剪纸图案中,属于轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
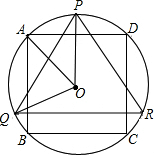 如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=
如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=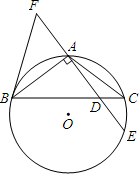 如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,AE⊥AB交BC于点D,交⊙O于点E,F在DA的延长线上,且AF=AD.
如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,AE⊥AB交BC于点D,交⊙O于点E,F在DA的延长线上,且AF=AD.