题目内容
下面方程中，有两个不等实数根的方程是（ ）
| A、x2+x-1=0 | ||
| B、x2-x+1=0 | ||
C、x2-x+
| ||
| D、x2+1=0 |
分析：分别计算各选项的△，来判断根的情况，一元二次方程有两个不等实数根即判别式的值大于0．
解答：解：A、∵△=b2-4ac=1+4=5＞0，
∴方程有两个不相等的实数根．
B、∵△=b2-4ac=1-4=-3＜0，
∴方程没有实数根．
C、∵△=b2-4ac=1-1=0，
∴方程有两个相等的实数根．
D、移项后得，x2=-1
∵任何数的平方一定是非负数．
∴方程无实根．故错误．
故选A．
∴方程有两个不相等的实数根．
B、∵△=b2-4ac=1-4=-3＜0，
∴方程没有实数根．
C、∵△=b2-4ac=1-1=0，
∴方程有两个相等的实数根．
D、移项后得，x2=-1
∵任何数的平方一定是非负数．
∴方程无实根．故错误．
故选A．
点评：总结：一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
相关题目
kx+k2-k+2=0，判别这个方程根的情况．”一题的解答过程，请你判断其是否正确，若有错误，请你写出正确解答．
kx+k2-k+2=0，判别这个方程根的情况．”一题的解答过程，请你判断其是否正确，若有错误，请你写出正确解答．
k）2-4×1×（k2-k+2）
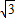kx+k2-k+2=0，判别这个方程根的情况．”一题的解答过程，请你判断其是否正确，若有错误，请你写出正确解答．
k）2-4×1×（k2-k+2）
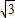kx+k2-k+2=0，判别这个方程根的情况．”一题的解答过程，请你判断其是否正确，若有错误，请你写出正确解答．
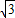k）2-4×1×（k2-k+2）