题目内容
(2003•宜昌)(1)下面是明明同学的作业中,对“已知关于x方程x2+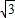 kx+k2-k+2=0,判别这个方程根的情况.”一题的解答过程,请你判断其是否正确,若有错误,请你写出正确解答.
kx+k2-k+2=0,判别这个方程根的情况.”一题的解答过程,请你判断其是否正确,若有错误,请你写出正确解答.解:△=(
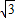 k)2-4×1×(k2-k+2)
k)2-4×1×(k2-k+2)=-k2+4k-8
=(k-2)2+4
∵(k-2)2≥0,4>0,∴△=(k-2)2+4>0
∴原方程有两个不相等的实数根.
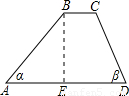
(2)如图,一防洪拦水坝的横断面为梯形ABCD,坝顶宽BC=3米,坝高BE=6米,坡角α为45°,坡角β为63°,求横断面(梯形ABCD)的面积.
【答案】分析:(1)根据判别式来判断根的情况时,计算的步骤要准确;
(2)过点C作CF⊥AD于F,利用直角三角形的特点来计算.
解答:解:(1)不正确.
△=(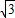 k)2-4×1×(k2-k+2)
k)2-4×1×(k2-k+2)
=-k2+4k-8
=-(k-2)2-4
∵-(k-2)2≤0,-4<0,
∴△=-(k-2)2-4<0
∴原方程无实数根.
(2)过点C作CF⊥AD于F,则BE=CF=6,
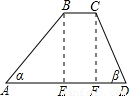 ∴AE=BE=6,
∴AE=BE=6,
又∵Rt△CDF中,∠α=63°,CF=6,
∴cot63°=DF:CF,
又∵CF=6,
∴DF=CF•cot63°=6×0.5=3,
∴AD=AE+EF+FD=6+3+3=12,
∴S梯形ABCD=12(BC+AD)•BE=12(3+12)×6=45(平方米).
答:梯形ABCD面积为45平方米.
点评:解答问题是步骤要正确,细致.第二题要用到解直角三角形的有关知识.
(2)过点C作CF⊥AD于F,利用直角三角形的特点来计算.
解答:解:(1)不正确.
△=(
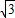 k)2-4×1×(k2-k+2)
k)2-4×1×(k2-k+2)=-k2+4k-8
=-(k-2)2-4
∵-(k-2)2≤0,-4<0,
∴△=-(k-2)2-4<0
∴原方程无实数根.
(2)过点C作CF⊥AD于F,则BE=CF=6,
 ∴AE=BE=6,
∴AE=BE=6,又∵Rt△CDF中,∠α=63°,CF=6,
∴cot63°=DF:CF,
又∵CF=6,
∴DF=CF•cot63°=6×0.5=3,
∴AD=AE+EF+FD=6+3+3=12,
∴S梯形ABCD=12(BC+AD)•BE=12(3+12)×6=45(平方米).
答:梯形ABCD面积为45平方米.
点评:解答问题是步骤要正确,细致.第二题要用到解直角三角形的有关知识.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
(2003•宜昌)汽车行驶中,司机从判断出现了紧急情况到进行刹车时,这一段汽车走过的路程称为刹车反应距离.某研究机构收集了有关刹车反应距离的数据如下表:
表中x为汽车行驶速度(英里/小时),y为刹车反应距离(英尺);m、n为丢失的数据.由表中给出的有序实数对,在直角坐标系中对应的点如图所示.
(1)请用平滑曲线顺次连接图中各点后,估计y与x的关系最近似于哪一种函数关系,并说明估计的理由;
(2)请利用估计得到的函数关系中,求出表中m、n的值.
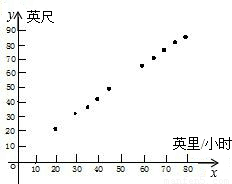
| x | 20 | 25 | 30 | 35 | 40 | 4 5 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
| y | 22 | m | 33 | 38.5 | 44 | 50 | 55 | n | 66 | 71 | 77 | 82.5 | 88 |
(1)请用平滑曲线顺次连接图中各点后,估计y与x的关系最近似于哪一种函数关系,并说明估计的理由;
(2)请利用估计得到的函数关系中,求出表中m、n的值.

(2003•宜昌)汽车行驶中,司机从判断出现了紧急情况到进行刹车时,这一段汽车走过的路程称为刹车反应距离.某研究机构收集了有关刹车反应距离的数据如下表:
表中x为汽车行驶速度(英里/小时),y为刹车反应距离(英尺);m、n为丢失的数据.由表中给出的有序实数对,在直角坐标系中对应的点如图所示.
(1)请用平滑曲线顺次连接图中各点后,估计y与x的关系最近似于哪一种函数关系,并说明估计的理由;
(2)请利用估计得到的函数关系中,求出表中m、n的值.

| x | 20 | 25 | 30 | 35 | 40 | 4 5 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
| y | 22 | m | 33 | 38.5 | 44 | 50 | 55 | n | 66 | 71 | 77 | 82.5 | 88 |
(1)请用平滑曲线顺次连接图中各点后,估计y与x的关系最近似于哪一种函数关系,并说明估计的理由;
(2)请利用估计得到的函数关系中,求出表中m、n的值.

 倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)
倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)
 倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)
倍时,你能确定k的值吗?若能,请求出k的值;若不能,请你说明理由.(图供分析参考用)
 ( )内可填入的是 .
( )内可填入的是 .