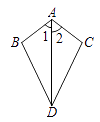
��Ŀ����
����Ŀ���ڵȱߡ�ABC�У�
��1����ͼ1��P��Q��BC�������㣬AP��AQ����BAP��20�㣬���AQB�Ķ�����
��2����P��Q��BC���ϵ���������(�����B��C�غ�)����P�ڵ�Q����࣬��AP��AQ����Q����ֱ��AC�ĶԳƵ�ΪM������AM��PM.
�������⽫ͼ2��ȫ����С��ͨ���۲졢ʵ�飬������룺�ڵ�P��Q�˶��Ĺ����У�ʼ����PA��PM��С�������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1��Ҫ֤PA��PM��ֻ��֤��APM�ǵȱ������Σ�
�뷨2����BA��ȡһ��N��ʹ��BN��BP��Ҫ֤PA��PM��ֻ��֤��ANP�ա�PCM.����
����ο�������뷨������С��֤��PA��PM(һ�ַ�������)��
���𰸡�
��1���⣺��AP��AQ�����APQ����AQP��
�֡ߡ�ABC�ǵȱ������Σ����B��60�㣬
�ߡ�BAP��20�㣬���AQB����APQ=��BAP����B��80��
��2���⣺����ͼ��
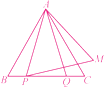
�����뷨1֤������AP=AQ��
���APQ=��AQP��
���APB=��AQC��
�ߡ�ABC�ǵȱ������Σ�
���B=��C=60�㣬
���BAP=��CAQ��
�ߵ�Q����ֱ��AC�ĶԳƵ�ΪM��
��AQ=AM����QAC=��MAC��
���MAC=��BAP��
���BAP+��PAC=��MAC+��CAP=60�㣬
���PAM=60�㣬
��AP=AQ��
��AP=AM��
���APM�ǵȱ������Σ�
��AP=PM��
�������뷨2֤������AB��ȡһ��N��ʹBN��BP������PN��CM��
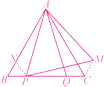
�ߡ�ABC�ǵȱ������Σ����B����ACB��60�㣬BA��BC��AC��
���BPN�ǵȱ������Σ�AN��PC��BP��NP����BNP��60�㣬
���ANP��120�㣬����Գ�֪CM��CQ����ACM����ACB��60�㣬
���PCM��120�㣬��(1)֪����APB����AQC�����ABP�ա�ACQ(AAS)��
��BP��CQ����NP��CM�����ANP�ա�PCM(SAS)����AP��PM.
����������1�����ݵȱ߶ԵȽǵó�����APQ����AQP�����ݵȱ������ε����ʣ��������ε���Ƕ����ó�����AQB����APQ=��BAP����B��80�� ��
��2������ͼ�����ݵȱ߶ԵȽǼ��ڲ��ǵĶ���ó���APB=��AQC �����ݵȱ������ε����ʵó���B=��C=60�㣬���������ε��ڽǺ͵ó���BAP=��CAQ��������ԳƵ����ʵó�AQ=AM����QAC=��MAC�����ݵ��������ó���MAC=��BAP �����ݵ�ʽ�����ʵó���BAP+��PAC=��MAC+��CAP=60�� ������PAM=60�㣬��AQ=AM ��AP=AQ����AP=AM��������һ������60![]() �ĵ����������ǵȱ������εó���APM�ǵȱ������Σ��Ӷ��ó����ۣ�AP=PM���������뷨2֤������AB��ȡһ��N��ʹBN��BP������PN��CM�����ݵȱ������ε����ʵó���B����ACB��60�㣬BA��BC��AC����һ���ó���BPN�ǵȱ������Σ�AN��PC��BP��NP����BNP��60�㣬�����첹�ǵĶ���ó���ANP��120�㣬�ɶԳƵ�֪ʶ�ó�CM��CQ����ACM����ACB��60�㣬�Ӷ��жϳ����ABP�ա�ACQ ������ȫ�������ε����ʵó�BP��CQ ���������ݵ��������ó�NP��CM���Ӷ��жϳ���ANP�ա�PCM ������ȫ�������ε����ʵó�AP��PM.
�ĵ����������ǵȱ������εó���APM�ǵȱ������Σ��Ӷ��ó����ۣ�AP=PM���������뷨2֤������AB��ȡһ��N��ʹBN��BP������PN��CM�����ݵȱ������ε����ʵó���B����ACB��60�㣬BA��BC��AC����һ���ó���BPN�ǵȱ������Σ�AN��PC��BP��NP����BNP��60�㣬�����첹�ǵĶ���ó���ANP��120�㣬�ɶԳƵ�֪ʶ�ó�CM��CQ����ACM����ACB��60�㣬�Ӷ��жϳ����ABP�ա�ACQ ������ȫ�������ε����ʵó�BP��CQ ���������ݵ��������ó�NP��CM���Ӷ��жϳ���ANP�ա�PCM ������ȫ�������ε����ʵó�AP��PM.