题目内容
【题目】已知点A、B在半径为1的⊙O上,直线AC与⊙O相切,OC⊥OB,连接AB交OC于点D.
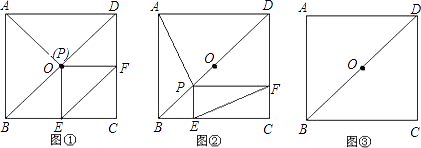
(Ⅰ)如图①,若∠OCA=60°,求OD的长;
(Ⅱ)如图②,OC与⊙O交于点E,若BE∥OA,求OD的长.

【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)如图①,先由切线得∠OAB+∠BAC=90°,再利用OC⊥OB的∠BOC=90°,然后根据对顶角相等和等腰三角形的形式可求解;
(2)先判断△OEB为等腰直角三角形,得到∠OBE=∠OEB=45°,然后根据平行线的性质可得∠DAC=∠ADC,可得AC=CD=1,OC=![]() OA=
OA=![]() ,由此得解.
,由此得解.
试题解析:(1)∵AC与⊙O相切,∴∠OAC=90°.
∵∠OCA=60°,∴∠AOC=30°.∵OC⊥OB,∴∠AOB=∠AOC+∠BOC=120°.
∵OA=OB,∴∠OAB=∠OBA=30°,∴OD=AD,∠DAC=60°∴AD=CD=AC.
∵OA=1,∴OD=AC=OAtan∠AOC=![]() .
.
(2)∵OC⊥OB,∴∠OBE=∠OEB=45°.∵BE∥OA,∴∠AOC=45°,∠ABE=∠OAB,
∴OA=AC,∠OAB=∠OBA=22.5°,∴∠ADC=∠AOC+∠OAB=67.5°.
∵∠DAC=90°﹣∠OAB=67.5°=∠ADC,∴AC=CD.∵OC=![]() =
=![]() ,∴OD=OC﹣CD=
,∴OD=OC﹣CD=![]() ﹣1.
﹣1.

练习册系列答案
相关题目