Question

【题目】如图,在△ABC中,DE是AC的垂直平分线.

（1）若AE=6,则AC＝　　　；

（2）若∠ABD=40，∠ADB=70，求∠BAC的度数.

Answer 1

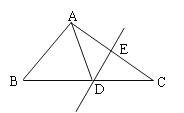
【答案】（1）12；（2）∠BAC＝105°

【解析】试题分析：（1）由线段垂直平分线的性质可得：AE=CE，即可求得AC值；

（2）由线段垂直平分线的性质得DA＝DC，由等边对等角，得∠DAC＝∠C，由外角的性质，可求得∠C＝35°，再由三角形外角和定理可得∠BAC度数.

试题解析：（1）∵DE是AC的垂直平分线，

∴AE=CE=6，

∴AC=2AE=12；

故答案为：12；

(2) ∵DE是AC的垂直平分线,

∴DA＝DC，

∴∠DAC＝∠C，

又∵∠ADB为△ADC的外角，

∴∠DAC＋∠C＝∠ADB=70，

∴∠DAC＝∠C＝35°，

在△ABC中，∠BAC＋∠ABD＋∠C＝180°.

∴∠BAC＝180°－∠ABD－∠C＝180°－40－35°＝105°.