题目内容
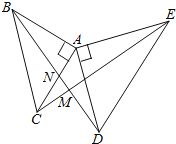
【题目】意大利文艺复兴时期的著名画家达芬奇利用两张一样的纸片拼出不一样的“空洞”,从而巧妙的证明了勾股定理.小明用两张全等的的纸片①和②拼成如图1所示的图形,中间的六边形![]() 由两个正方形和两个全等的直角三角形组成.已知六边形
由两个正方形和两个全等的直角三角形组成.已知六边形![]() 的面积为28,
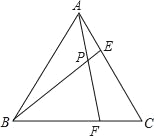
的面积为28,![]() .小明将纸片②翻转后拼成如图2所示的图形,其中
.小明将纸片②翻转后拼成如图2所示的图形,其中![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )

A.16B.20C.22D.24
【答案】B
【解析】
根据图形及勾股定理的验证得到BC2=BG2+CG2,故四边形![]() 的面积等于四边形
的面积等于四边形![]() 的面积加上四边形
的面积加上四边形![]() 的面积,再根据六边形
的面积,再根据六边形![]() 的面积为28,
的面积为28,![]() 即可求解.
即可求解.
∵![]()
∴可设BG=2a,CG=a,
∵六边形![]() 的面积为28,
的面积为28,
∴4a2+a2+ ![]() =28
=28
解得a=2(-2)舍去,
根据图形及勾股定理的验证得到BC2=BG2+CG2,
∴四边形![]() 的面积=四边形
的面积=四边形![]() 的面积加上四边形
的面积加上四边形![]() 的面积=4a2+a2=5×4=20
的面积=4a2+a2=5×4=20
故选B.

练习册系列答案
相关题目
【题目】某甜品店用![]() ,
,![]() 两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品
两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品![]() 份,乙款甜品
份,乙款甜品![]() 份,共用去
份,共用去![]() 原料2000克.
原料2000克.
原料 款式 |
(克) |
(克) |
甲款甜品 | 30 | 15 |
乙款甜品 | 10 | 20 |
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)已知每份甲甜品的利润为5元,每份乙甜品的利润为2元.假设两款甜品均能全部卖出.若获得总利润不少于360元,则至少要用去![]() 原料多少克?
原料多少克?