题目内容
【题目】如图1，点P为四边形ABCD所在平面上的点，如果∠PAD=∠PBC，则称点P为四边形ABCD关于A、B的等角点，以点C为坐标原点，BC所在直线为
轴建立平面直角坐标系，点B的横坐标为﹣6．
（1）如图2，若A、D两点的坐标分别为A（﹣6，4）、D（0，4），点P在DC边上，且点P为四边形ABCD关于A、B的等角点，则点P的坐标为 _________ ；
（2）如图3，若A、D两点的坐标分别为A（﹣2，4）、D（0，4）．
①若P在DC边上时，则四边形ABCD关于A、B的等角点P的坐标为 _________ ；
②在①的条件下，将PB沿
轴向右平移
个单位长度（0＜
＜6）得到线段P′B′，连接P′D，B′D，试用含
的式子表示P′D2+B′D2，并求出使P′D2+B′D2取得最小值时点P′的坐标；
③如图4，若点P为四边形ABCD关于A、B的等角点，且点P坐标为（1， 
），求
的值；
④以四边形ABCD的一边为边画四边形，所画的四边形与四边形ABCD有公共部分，若在所画的四边形内存在一点P，使点P分别是各相邻两顶点的等角点，且四对等角都相等，请直接写出所有满足条件的点P的坐标．
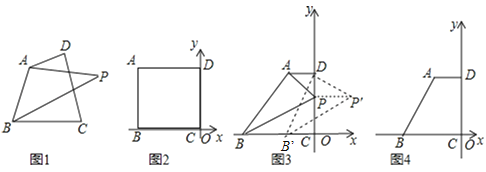
【答案】（1）（0，2）；（2）①（0，3）；②2m2-12m+53，（3，3）；③2.8；④（-1，3），（-2，2），（-3，3），（-2，0）
【解析】试题分析：（1）连结AP，BP，由全等三角形的性质就可以得出PD=PC而得出结论；
（2）①由△ADP∽△BCP就可以得出
而求出结论；
②求出代表P′D2+B′D2的方程式，并求最小值．
③画图求证△PAM∽△PBN，值得注意的是本题有两个图形，容易漏掉一个答案．
④由题意可知，必须是正方形才能满足题干要求．
试题解析：解：（1）由B点坐标（﹣6，0），A点坐标（﹣6，4）、D点坐标（0，4），可以得出四边形ABCD为矩形，
∵P在CD边上，且∠PAD=∠PBC，∠ADP=∠BCP，BC=AD；
∴△ADP≌△BCP，∴CP=DP，
∴P点坐标为（0，2）；
（2）①∵∠DAP=∠CBP，∠BCP=∠ADP=90°，
∴△ADP∽△BCP，
∴
=
=
，
∴CP=3DP，∴CP=3，DP=1，
∴P点坐标为（0，3）；
②如图3，由题意，易得 B′（m﹣6，0），P′（m，3）
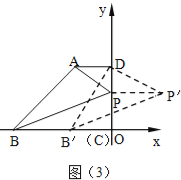
由勾股定理得P′D2+B′D2=PP′2+PD2+OD2+B′C2=m2+（4﹣3）2+42+（m﹣6）2=2m2﹣12m+53，
∵2＞0
∴P′D2+B′D2有最小值，
当m=﹣
=3时，（在0＜m＜6范围内）时，P′D2+B′D2有最小值，此时P′坐标为（3，3）；
③由题意知，点P在直线x=1上，延长AD交直线x=1于M，
（a）如图，当点P在线段MN上时，易证△PAM∽△PBN，
∴
，
即
，
解得t=2．8
(b）如图，当点P为BA的延长线与直线x=1的交点时，易证△PAM∽△PBN，
∴
，即
，解得t=7，
综上可得，t=2．8或t=7；
④因满足题设条件的四边形是正方形，
故所求P的坐标为（﹣1，3），（﹣2，2），（﹣3，3），（﹣2，0）．
