题目内容
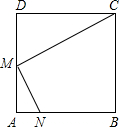 已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.
已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.
分析:两个三角形都是直角三角形,还只需满足一对角对应相等或夹直角的两边对应成比例即可说明两个三角形相似.
若DM与AM对应,则△CDM与△MAN全等,N与B重合,不合题意;
若DM与AN对应,则CD:AM=DM:AN,得AN=
a,从而确定N的位置.
若DM与AM对应,则△CDM与△MAN全等,N与B重合,不合题意;
若DM与AN对应,则CD:AM=DM:AN,得AN=
| 1 |
| 4 |
解答:证明:分两种情况讨论:
①若△CDM∽△MAN,则
=
.
∵边长为a,M是AD的中点,
∴AN=
a.
②若△CDM∽△NAM,则
=
.
∵边长为a,M是AD的中点,
∴AN=a,即N点与B重合,不合题意.
所以,能在边AB上找一点N(不含A、B),使得△CDM与△MAN相似.当AN=
a时,N点的位置满足条件.
①若△CDM∽△MAN,则
| DM |
| AN |
| CD |
| AM |
∵边长为a,M是AD的中点,
∴AN=
| 1 |
| 4 |
②若△CDM∽△NAM,则
| CD |
| AN |
| DM |
| AM |
∵边长为a,M是AD的中点,
∴AN=a,即N点与B重合,不合题意.
所以,能在边AB上找一点N(不含A、B),使得△CDM与△MAN相似.当AN=
| 1 |
| 4 |
点评:此题考查相似三角形的判定.因不明确对应关系,所以需分类讨论.

练习册系列答案
相关题目
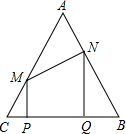 已知:如图,在边长为2的等边三角形△ABC中,点P以每秒1个单位从C向B运动,运动时间为t秒,且PQ=1,过P、Q点分别向BC作垂线,垂足分别为P、Q,交AC、AB于M、N,连接MN;
已知:如图,在边长为2的等边三角形△ABC中,点P以每秒1个单位从C向B运动,运动时间为t秒,且PQ=1,过P、Q点分别向BC作垂线,垂足分别为P、Q,交AC、AB于M、N,连接MN; 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
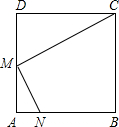 已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.
已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由. 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.