题目内容
已知：如图，在边长为a的正△ABC中，分别以A，B，C点为圆心，
长为半径作
，
，
，求阴影部分的面积．
【答案】分析：根据等边三角形的性质求出扇形ADE的面积，再根据S阴影=S△ABC-3S扇形ADE进行解答即可．
解答：解：∵△ABC是等边三角形，
∴∠A=60°，
∴S阴影=S△ABC-3S扇形ADE
=
a2•asin60°-3×
=
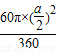
a2×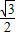
-
=
-
=
．
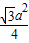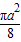
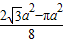点评：本题考查的是扇形面积的计算及等边三角形的性质，根据题意得出S阴影=S△ABC-3S扇形ADE是解答此题的关键．
解答：解：∵△ABC是等边三角形，
∴∠A=60°，
∴S阴影=S△ABC-3S扇形ADE
=
a2•asin60°-3×=
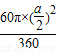
a2×-=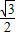
-=
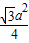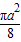
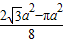．点评：本题考查的是扇形面积的计算及等边三角形的性质，根据题意得出S阴影=S△ABC-3S扇形ADE是解答此题的关键．
练习册系列答案
春雨教育同步作文系列答案
相关题目
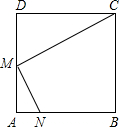已知，如图，在边长为a的正方形ABCD中，M是AD的中点，能否在边AB上找一点N（不含A、B），使得△CDM与△MAN相似？若能，请给出证明，若不能，请说明理由．
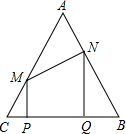已知：如图，在边长为2的等边三角形△ABC中，点P以每秒1个单位从C向B运动，运动时间为t秒，且PQ=1，过P、Q点分别向BC作垂线，垂足分别为P、Q，交AC、AB于M、N，连接MN；
已知：如图，在边长为a的正△ABC中，分别以A，B，C点为圆心，
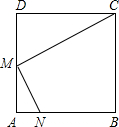已知，如图，在边长为a的正方形ABCD中，M是AD的中点，能否在边AB上找一点N（不含A、B），使得△CDM与△MAN相似？若能，请给出证明，若不能，请说明理由．