��Ŀ����
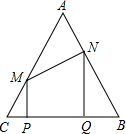 ��֪����ͼ���ڱ߳�Ϊ2�ĵȱ������Ρ�ABC�У���P��ÿ��1����λ��C��B�˶����˶�ʱ��Ϊt�룬��PQ=1����P��Q��ֱ���BC�����ߣ�����ֱ�ΪP��Q����AC��AB��M��N������MN��
��֪����ͼ���ڱ߳�Ϊ2�ĵȱ������Ρ�ABC�У���P��ÿ��1����λ��C��B�˶����˶�ʱ��Ϊt�룬��PQ=1����P��Q��ֱ���BC�����ߣ�����ֱ�ΪP��Q����AC��AB��M��N������MN����1����tΪ��ֵʱ���ı���MPQN�Ǿ��Σ�
��2�����ܵ�P����ƶ����ı���MPQN������Ƿ�ı䣬˵�����ɣ�
��3����tΪ��ֵʱ����CMP���AMN���ƣ���ʱ��MNP��ʲô���͵������Σ�
��������1�������ı���MPQN�Ǿ��Σ�������MPQN��PM=NQ���ݴ��г�����t�ĵ�ʽ���ⷽ�̼��ɣ�
��2�����ܵ�P����ƶ����ı���MPQN������������ı䣬���ݣ�1��������PM��QN�ı���ʽ�����������������ʽ�������S����t�ĺ�����ϵʽ��ͨ������Ϊ��ֵ��
��3�����ݶ�Ӧ��Ͷ�Ӧ�ߵIJ�ͬ����õ���ͬ�����������Σ��ٷ�����������ۣ�
��2�����ܵ�P����ƶ����ı���MPQN������������ı䣬���ݣ�1��������PM��QN�ı���ʽ�����������������ʽ�������S����t�ĺ�����ϵʽ��ͨ������Ϊ��ֵ��
��3�����ݶ�Ӧ��Ͷ�Ӧ�ߵIJ�ͬ����õ���ͬ�����������Σ��ٷ�����������ۣ�
����⣺��1���ߡ�ABC�ǵȱ������Σ�PM��CB��QN��CB��
���B=��C=60�㣬
��Rt��CPM��Rt��BQN��
��CP=t��BQ=1-t��
��PM=CP•tanC=t•tan60��=
t��
QN=BQ•tanB=��1-t��tan60��=
��1-t����
���ı���MPQN�Ǿ��Σ�
��PM=NQ��
����
t=
��1-t����
��ã�t=
��
��2�����ܵ�P����ƶ����ı���MPQN������������ı䣬�������£�
�ɣ�1����֪��PM=CP•tanC=t•tan60��=
t��QN=BQ•tanB=��1-t��tan60��=
��1-t����
��S�ı���MPNQ=
��1��[
t+
��1-t��]=
��
��ܵ�P����ƶ����ı���MPQN������������ı䣻
��3���ߡ�CMP��Rt�����ҡ�CPM=90�㣬��C=60�㣬��AMN�С�A=60�㣬
��ʹ��CMP���AMN���ƣ���Ӧ�Ķ���ֻ���ǣ�C��A��P��N��M��M��C��A��P��M��M��N��
�ٵ�C��A��P��N��M��Mʱ���ɡ�CMP�ס�AMN�ã�
��CM=2t��BN=2��1-t��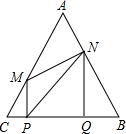 ��
��
��AM=2-2t��AN=2-2��1-t��=2t��
��
=
��
��ã�t=
��
�ڵ�C��A��P��M��M��Nʱ���ɡ�CMP�ס�ANM�ã�
=
��
��
=
����ã�t=
��
�ۺϣ�����t=
��
ʱ��CMP���AMN���ƣ�
��t=
ʱ������AM=CP=BN��AN=CM=BP��
�ҡ�A=��B=��C=60�㣬
���ANM�ա�CMP�ա�BPN��
��NM=MP=PN������MNP�ǵȱ������Σ�
���B=��C=60�㣬
��Rt��CPM��Rt��BQN��
��CP=t��BQ=1-t��
��PM=CP•tanC=t•tan60��=
| 3 |
QN=BQ•tanB=��1-t��tan60��=
| 3 |
���ı���MPQN�Ǿ��Σ�
��PM=NQ��
����
| 3 |
| 3 |
��ã�t=
| 1 |
| 2 |
��2�����ܵ�P����ƶ����ı���MPQN������������ı䣬�������£�
�ɣ�1����֪��PM=CP•tanC=t•tan60��=
| 3 |
| 3 |
��S�ı���MPNQ=
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
��ܵ�P����ƶ����ı���MPQN������������ı䣻
��3���ߡ�CMP��Rt�����ҡ�CPM=90�㣬��C=60�㣬��AMN�С�A=60�㣬
��ʹ��CMP���AMN���ƣ���Ӧ�Ķ���ֻ���ǣ�C��A��P��N��M��M��C��A��P��M��M��N��
�ٵ�C��A��P��N��M��Mʱ���ɡ�CMP�ס�AMN�ã�
��CM=2t��BN=2��1-t��
 ��
����AM=2-2t��AN=2-2��1-t��=2t��
��
| t |
| 2t |
| 2t |
| 2-2t |
��ã�t=
| 1 |
| 3 |
�ڵ�C��A��P��M��M��Nʱ���ɡ�CMP�ס�ANM�ã�
| CP |
| AM |
| CM |
| AN |
��
| 2t |
| 2-2t |
| 2t |
| 2t |
| 2 |
| 3 |
�ۺϣ�����t=
| 1 |
| 3 |
| 2 |
| 3 |
��t=
| 2 |
| 3 |
�ҡ�A=��B=��C=60�㣬
���ANM�ա�CMP�ա�BPN��
��NM=MP=PN������MNP�ǵȱ������Σ�
���������⿼���˵ȱ������ε������Լ��ж�������ǵ�������Ǻ���ֵ�����ε����ʡ����������ε��ж������ʣ�������һ���������⣬����Ĺؼ��dz���������������ε����ʺ;��ε������г�����t�ĵ�ʽ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
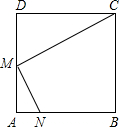 ��֪����ͼ���ڱ߳�Ϊa��������ABCD�У�M��AD���е㣬�ܷ��ڱ�AB����һ��N������A��B����ʹ�á�CDM���MAN���ƣ����ܣ������֤���������ܣ���˵�����ɣ�
��֪����ͼ���ڱ߳�Ϊa��������ABCD�У�M��AD���е㣬�ܷ��ڱ�AB����һ��N������A��B����ʹ�á�CDM���MAN���ƣ����ܣ������֤���������ܣ���˵�����ɣ� ��֪����ͼ���ڱ߳�Ϊa������ABC�У��ֱ���A��B��C��ΪԲ�ģ�
��֪����ͼ���ڱ߳�Ϊa������ABC�У��ֱ���A��B��C��ΪԲ�ģ�
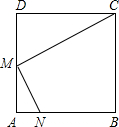 ��֪����ͼ���ڱ߳�Ϊa��������ABCD�У�M��AD���е㣬�ܷ��ڱ�AB����һ��N������A��B����ʹ�á�CDM���MAN���ƣ����ܣ������֤���������ܣ���˵�����ɣ�
��֪����ͼ���ڱ߳�Ϊa��������ABCD�У�M��AD���е㣬�ܷ��ڱ�AB����һ��N������A��B����ʹ�á�CDM���MAN���ƣ����ܣ������֤���������ܣ���˵�����ɣ� ��Ϊ�뾶��
��Ϊ�뾶�� ��
�� ��
�� ������Ӱ���ֵ������
������Ӱ���ֵ������