题目内容
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC.
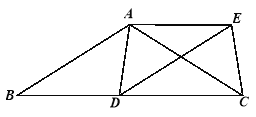
(1)求证:AD=EC;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
【答案】(1)、证明过程见解析;(2)、点D是BC的中点,证明过程见解析.
【解析】
试题分析:(1)、根据平移得到AD平行且等于DE,∠B=∠EDC,根据AB=AC得出∠B=∠ACD,AC=DE,结合DC=CD得到△ACD和△ECD全等,得出AD=EC;(2)、首先得出四边形ADCE是平行四边形,结合AD⊥BC得出矩形.
试题解析:(1)、由平移可得AB∥DE,AB=DE; ∴∠B=∠EDC∵ AB=AC ∴∠B=∠ACD, AC=DE
∴∠EDC =∠ACD ∵DC=CD ∴△ACD≌△ECD(SAS) ∴AD=EC
(2)、当点D是BC中点时,四边形ADCE是矩形
理由如下:∵AB=AC,点D是BC中点 ∴BD=DC,AD⊥BC
由平移性质可知 四边形ABDE是平行四边形 ∴AE=BD,AE∥BD ∴AE=DC,AE∥DC
∴四边形ADCE是平行四边形 ∵AD⊥BC ∴四边形ADCE是矩形

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目