题目内容
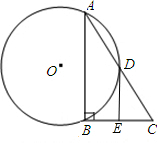
已知:AB是⊙O的弦,OD⊥AB于M交⊙O于点D,CB⊥AB交AD的延长线于C.
(1)求证:AD=DC;
(2)过D作⊙O的切线交BC于E,若DE=2,CE=1,求⊙O的半径.
(1)证明:在⊙O中,OD⊥AB,CB⊥AB,
∴AM=MB,OD∥BC. …………………1分
∴AD=DC. ……………2分
(2)∵DE为⊙O切线,
∴OD⊥DE ……………3分
∴四边形MBED为矩形.
∴DE∥AB. ……………4分
∴MB=DE=2,MD=BE=EC=1.
连接OB.
在Rt△OBM中,OB2=OM2+BM2.
解得 OB= . …………………5分
解析:略

练习册系列答案
相关题目
 已知:AB是⊙O的弦,D是
已知:AB是⊙O的弦,D是
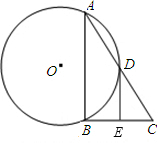 已知:AB是⊙O的弦,D是
已知:AB是⊙O的弦,D是 如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是
如图,已知:AB是⊙O的弦,C是AB上的点,AC=4、BC=1、OC=2,则⊙O的半径是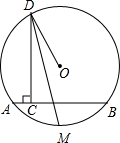 如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.
如图,已知:AB是⊙O的弦,D为⊙O上一点,DC⊥AB于C,DM平分∠CDO.求证:M是弧AB的中点.