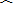题目内容
已知线段AB是⊙O的弦,点P是优弧 |
| AB |
(1)画图并证明:当点P在优弧
 |
| AB |
(2)当点P在优弧
 |
| AB |
分析:(1)由∠APQ=∠BPQ,根据圆周角定理得到弧AQ=弧BQ,即Q为弧AB的中点,为定点;
(2)由于AQ为定值,所以当P到AQ的距离最大时,△APQ的面积取得最大值,则过圆心O作AQ的垂线交优弧AB于P点.
(2)由于AQ为定值,所以当P到AQ的距离最大时,△APQ的面积取得最大值,则过圆心O作AQ的垂线交优弧AB于P点.
解答: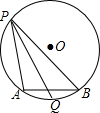 证明:(1)如图,
证明:(1)如图,
∵∠APQ=∠BPQ,
∴弧AQ=弧BQ,
∴Q为弧AB的中点,
即∠APB的平分线过定点Q.
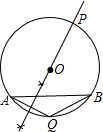
(2)能取得最大值.理由如下:
∵AQ为定值,
∴当P到AQ的距离最大时,△APQ的面积取得最大值,
所以过圆心O作AQ的垂线交优弧AB于P点.如图.
 证明:(1)如图,
证明:(1)如图,∵∠APQ=∠BPQ,
∴弧AQ=弧BQ,
∴Q为弧AB的中点,
即∠APB的平分线过定点Q.

(2)能取得最大值.理由如下:
∵AQ为定值,
∴当P到AQ的距离最大时,△APQ的面积取得最大值,
所以过圆心O作AQ的垂线交优弧AB于P点.如图.
点评:本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.也考查了圆周角定理以及过一点作直线的垂线的方法.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 上一个动点(P不与A、B重合),直线l是∠APB的平分线.
上一个动点(P不与A、B重合),直线l是∠APB的平分线.