题目内容
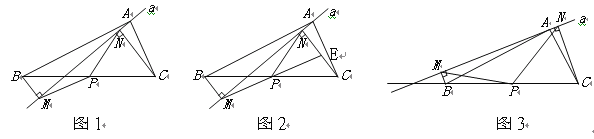
【题目】如图1，在△ABC中，点P为BC边中点，直线a绕顶点A旋转，若B、P在直线a的异侧，BM直线a于点M，CN直线a于点N，连接PM、PN；
(1) 延长MP交CN于点E(如图2)。求证：△BPM≌△CPE；求证：PM=PN；
(2) 若直线a绕点A旋转到图3的位置时，点B、P在直线a的同侧，其它条件不变。此时
PM=PN还成立吗？若成立，请给予证明；若不成立，请说明理由；
(3) 若直线a绕点A旋转到与BC边平行的位置时，其它条件不变。请直接判断四边形MBCN
的形状及此时PM=PN还成立吗？不必说明理由。
【答案】（1）见解析；（2）成立；（3）成立
【解析】
试题分析：（1）①根据平行线的性质证得∠MBP=∠ECP再根据BP=CP，∠BPM=∠CPE即可得到；
②由△BPM≌△CPE，得到PM=PE则PM=
ME，而在Rt△MNE中，PN=
ME，即可得到PM=PN．
（2）证明方法与②相同．
（3）四边形MBCN是矩形，则PM=PN成立．
（1）①如图2：
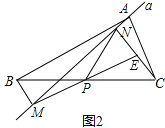
∵BM⊥直线a于点M，CN⊥直线a于点N，
∴∠BMA=∠CNM=90°，
∴BM∥CN，
∴∠MBP=∠ECP，
又∵P为BC边中点，
∴BP=CP，
又∵∠BPM=∠CPE，
∴△BPM≌△CPE，
②∵△BPM≌△CPE，
∴PM=PE
∴PM=ME，
∴在Rt△MNE中，PN=ME，
∴PM=PN．
（2）成立，如图3，延长MP与NC的延长线相交于点E，
∵BM⊥直线a于点M，CN⊥直线a于点N，
∴∠BMN=∠CNM=90°
∴∠BMN+∠CNM=180°，
∴BM∥CN
∴∠MBP=∠ECP，
又∵P为BC中点，
∴BP=CP，
又∵∠BPM=∠CPE，
∴△BPM≌△CPE，
∴PM=PE，
∴PM=ME，
则Rt△MNE中，PN=ME，
∴PM=PN．
（3）如图4：
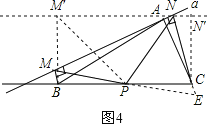
四边形M′BCN′是矩形，
根据矩形的性质和P为BC边中点，得到△M′BP≌△N′CP，
得PM′=PN′成立．即“四边形MBCN是矩形，则PM=PN成立”．
