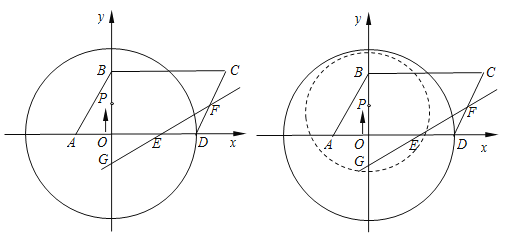题目内容
【题目】如图,直线![]() 与x轴交于点A(1,0),与 y交于点B(0,-2).
与x轴交于点A(1,0),与 y交于点B(0,-2).
(1)求直线AB的表达式;
(2)点C是直线AB上的点,且CA=AB,过动点P(m,0)且垂直于x轴的直线与直线AB 交于点D,若点D不在线段BC上,写出m的取值范围.
【答案】(1) 直线AB的表达式是y=2x-2 ;
(2)m<0或 m﹥2
【解析】试题分析:(1)直接将A、B两点坐标代入![]() 中,解方程即可;(2)过点C 作CE ⊥x 轴,垂足是E,求出点C的坐标,即可写出m的取值范围;
中,解方程即可;(2)过点C 作CE ⊥x 轴,垂足是E,求出点C的坐标,即可写出m的取值范围;
试题解析:
(1) 解:将 A(1,0),B(0,-2)代入 ![]() 得,
得,
![]()
∴b=-2 ,k=2
∴直线AB的表达式是y=2x-2
(2) 过点C 作CE ⊥x 轴,垂足是E,如图所示:
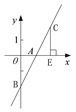
∵CA=AB
∠BOA = ∠AEC= 90°
∠BOA = ∠CAE
∴△BOA≌△CAE
∴CE=AB=2, AE=OA=1
∴C(2,2)
由图示知,m<0或 m﹥2

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
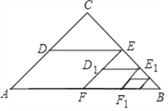
【题目】正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):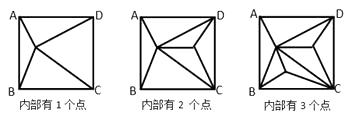
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)原正方形能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.