题目内容
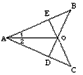
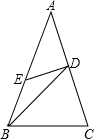 已知:如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,则∠A的度数是
已知:如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,则∠A的度数是
- A.30°
- B.36°
- C.45°
- D.50°
C
分析:根据AB=AC,BC=BD,AD=DE=EB可得到几组相等的角,再根据三角形外角的性质可得到∠C,∠A,∠EBD之间的关系,再根据三角形内角和定理即可求解.
解答:设∠EBD=x°,
∵BE=DE,
∴∠EDB=∠EBD=x°,
∴∠AED=∠EBD+∠EDB=2x°,
∵AD=DE,
∴∠A=∠AED=2x°,
∴∠BDC=∠A+∠ABD=3x°,
∵BD=BC,
∴∠C=∠BDC=3x°,
∵AB=AC,
∴∠ABC=∠C=3x°,
∵∠A+∠ABC+∠C=180°,
∴2x+3x+3x=180,
解得:x=22.5,
∴∠A=2x°=45°.
故选C.
点评:此题主要考查等腰三角形的性质,三角形外角的性质及三角形内角和定理的综合运用.
分析:根据AB=AC,BC=BD,AD=DE=EB可得到几组相等的角,再根据三角形外角的性质可得到∠C,∠A,∠EBD之间的关系,再根据三角形内角和定理即可求解.
解答:设∠EBD=x°,
∵BE=DE,
∴∠EDB=∠EBD=x°,
∴∠AED=∠EBD+∠EDB=2x°,
∵AD=DE,
∴∠A=∠AED=2x°,
∴∠BDC=∠A+∠ABD=3x°,
∵BD=BC,
∴∠C=∠BDC=3x°,
∵AB=AC,
∴∠ABC=∠C=3x°,
∵∠A+∠ABC+∠C=180°,
∴2x+3x+3x=180,
解得:x=22.5,
∴∠A=2x°=45°.
故选C.
点评:此题主要考查等腰三角形的性质,三角形外角的性质及三角形内角和定理的综合运用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
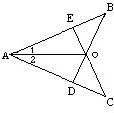 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,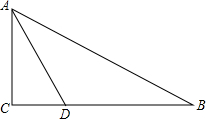 (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.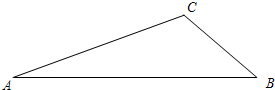 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.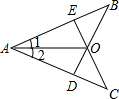 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,