题目内容
(2004•枣庄)如图,函数y=ax2+bx+c(其中a,b,c为常数)的图象分别与x轴,y轴交于A,B,C三点,M为抛物线的顶点,且AC⊥BC,OA<OB.(1)试确定a,b,c的符号;
(2)求证:b2-4ac>4;
(3)当b=2时,M点与经过A,B,C三点的圆的位置关系如何?证明你的结论.注:y=ax2+bx+c的对称轴为
 ,顶点为
,顶点为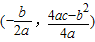 .
.
【答案】分析:(1)抛物线与y轴的交点在y轴正半轴,首先可以确定的是c>0.由于抛物线与x轴的两交点在原点两侧,如果设(x1,0),B(x2,0)的话,那么根据x1x2= <0,由此可确定a的符号.由于抛物线对称轴在y轴右侧,因此抛物线的对称轴方程大于0,据此可求出b的符号;
<0,由此可确定a的符号.由于抛物线对称轴在y轴右侧,因此抛物线的对称轴方程大于0,据此可求出b的符号;
(2)根据圆周角定理,可得出∠ACB=90°,在直角三角形ACB中,根据射影定理可得出OC2=OA•OB,即c2=-x1x2=- ,由此可得出ac=-1,代入b2-4ac中即可得出证的条件;
,由此可得出ac=-1,代入b2-4ac中即可得出证的条件;
(3)将b的值代入抛物线的解析式中,表示出M点和圆心的坐标,进而可求出圆的半径,然后比较圆的半径和M点纵坐标的大小关系即可.
解答:解:(1)∵抛物线与y轴的交点在y轴正半轴,
∴c>0,x1x2=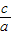 <0,a<0,
<0,a<0,
由于抛物线对称轴在y轴右侧,
因此抛物线的对称轴方程大于0,
即- >0,b>0.
>0,b>0.
∴a<0,b>0,c>0;
(2)设A(x1,0),B(x2,0),
则x1+x2=- ,x1x2=
,x1x2= ,
,
∵AC⊥CB,且C点坐标为(0,c),
∴Rt△AOC∽Rt△COB,
∴ ,
,
即x1x2=-c2= ,
,
∴ac=-1,
∴b2-4ac=b2+4>4;
(3)M点在经过A,B,C三点的圆外,
理由如下:当b=2时, ,
,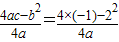 =
= ,
,
∵AC⊥CB,
∴经过A,B,C三点的圆的圆心为AB的中点D(- ,0),
,0),
半径为DC=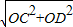 =
= =
= =-
=-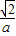 ,
,
又∵M点的坐标为(- ,-
,- ),且a<0,
),且a<0,
∴DM=- >-
>- =DC,
=DC,
∴M点在经过A,B,C三点的圆外.
点评:本题主要考查了二次函数与一元二次方程的关系、韦达定理的应用以及点与圆的位置关系等知识.
 <0,由此可确定a的符号.由于抛物线对称轴在y轴右侧,因此抛物线的对称轴方程大于0,据此可求出b的符号;
<0,由此可确定a的符号.由于抛物线对称轴在y轴右侧,因此抛物线的对称轴方程大于0,据此可求出b的符号;(2)根据圆周角定理,可得出∠ACB=90°,在直角三角形ACB中,根据射影定理可得出OC2=OA•OB,即c2=-x1x2=-
 ,由此可得出ac=-1,代入b2-4ac中即可得出证的条件;
,由此可得出ac=-1,代入b2-4ac中即可得出证的条件;(3)将b的值代入抛物线的解析式中,表示出M点和圆心的坐标,进而可求出圆的半径,然后比较圆的半径和M点纵坐标的大小关系即可.
解答:解:(1)∵抛物线与y轴的交点在y轴正半轴,
∴c>0,x1x2=
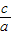 <0,a<0,
<0,a<0,由于抛物线对称轴在y轴右侧,
因此抛物线的对称轴方程大于0,
即-
 >0,b>0.
>0,b>0.∴a<0,b>0,c>0;
(2)设A(x1,0),B(x2,0),
则x1+x2=-
 ,x1x2=
,x1x2= ,
,∵AC⊥CB,且C点坐标为(0,c),
∴Rt△AOC∽Rt△COB,
∴
 ,
,即x1x2=-c2=
 ,
,∴ac=-1,
∴b2-4ac=b2+4>4;
(3)M点在经过A,B,C三点的圆外,
理由如下:当b=2时,
 ,
,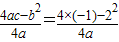 =
= ,
,∵AC⊥CB,
∴经过A,B,C三点的圆的圆心为AB的中点D(-
 ,0),
,0),半径为DC=
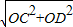 =
= =
= =-
=-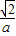 ,
,又∵M点的坐标为(-
 ,-
,- ),且a<0,
),且a<0,∴DM=-
 >-
>- =DC,
=DC,∴M点在经过A,B,C三点的圆外.
点评:本题主要考查了二次函数与一元二次方程的关系、韦达定理的应用以及点与圆的位置关系等知识.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
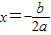 ,顶点为
,顶点为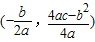 .
.


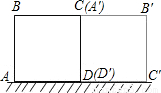
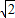 cm
cm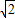 πcm
πcm