题目内容
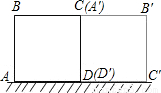
(2004•枣庄)如图,已知矩形ABCD中,CE⊥BD于E,CF平分∠DCE与DB交于点F,FG∥DA与AB交于点G.(1)求证:BF=BC;
(2)若AB=4cm,AD=3cm,求CF.

【答案】分析:(1)要求证:BF=BC只要证明∠CFB=∠FCB就可以,从而转化为证明∠BCE=∠BDC就可以;
(2)已知AB=4cm,AD=3cm,就是已知BC=BF=3cm,CD=4cm,在直角△BCD中,根据三角形的面积等于 BD•CE=
BD•CE= BC•DC,就可以求出CE的长.
BC•DC,就可以求出CE的长.
要求CF的长,可以在直角△CEF中用勾股定理求得.其中EF=BF-BE,BE在直角△BCE中根据勾股定理,就可以求出.
解答:(1)证明:∵四边形ABCD是矩形,
∴∠CDB+∠DBC=90°.
∵CE⊥BD,
∴∠DBC+∠ECB=90°.
∴∠ECB=∠CDB.
又∵∠DCF=∠ECF,
∴∠CFB=∠CDB+∠DCF=∠ECB+∠ECF=∠BCF.
∴BF=BC;
(2)解:在Rt△ABD中,由勾股定理得
BD=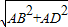 =
=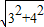 =5.
=5.
又∵BD•CE=BC•DC,
∴CE= .
.
∴ =
= .
.
∴EF=BF-BE=3- .
.
∴CF= .
.
点评:本题主要应用了等腰三角形的判定定理,等角对等边,以及勾股定理.
(2)已知AB=4cm,AD=3cm,就是已知BC=BF=3cm,CD=4cm,在直角△BCD中,根据三角形的面积等于
 BD•CE=
BD•CE= BC•DC,就可以求出CE的长.
BC•DC,就可以求出CE的长.要求CF的长,可以在直角△CEF中用勾股定理求得.其中EF=BF-BE,BE在直角△BCE中根据勾股定理,就可以求出.
解答:(1)证明:∵四边形ABCD是矩形,
∴∠CDB+∠DBC=90°.
∵CE⊥BD,
∴∠DBC+∠ECB=90°.
∴∠ECB=∠CDB.
又∵∠DCF=∠ECF,
∴∠CFB=∠CDB+∠DCF=∠ECB+∠ECF=∠BCF.
∴BF=BC;
(2)解:在Rt△ABD中,由勾股定理得
BD=
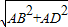 =
=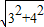 =5.
=5.又∵BD•CE=BC•DC,
∴CE=
 .
.∴
 =
= .
.∴EF=BF-BE=3-
 .
.∴CF=
 .
.点评:本题主要应用了等腰三角形的判定定理,等角对等边,以及勾股定理.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 ,顶点为
,顶点为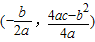 .
.
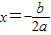 ,顶点为
,顶点为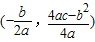 .
.

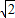 cm
cm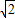 πcm
πcm