Question

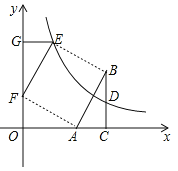
【题目】如图，在直角坐标系中，Rt△ABC的直角边AC在x轴上，∠ACB=90°，AC=1，反比例函数（k＞0）的图象经过BC边的中点D（3，1）．

（1）求这个反比例函数的表达式；

（2）若△ABC与△EFG成中心对称，且△EFG的边FG在y轴的正半轴上，点E在这个函数的图象上．

①求OF的长；

②连接AF，BE，证明四边形ABEF是正方形．

Answer 1

【答案】（1）；（2）①1；②证明见解析．

【解析】

试题分析：（1）由D点坐标可求得k的值，可求得反比例函数的表达式；

（2）①由中心对称的性质可知△ABC≌△EFG，由D点坐标可求得B点坐标，从而可求得BC和AC的长，由全等三角形的性质可求得GE和GF，则可求得E点坐标，从而可求得OF的长；②由条件可证得△AOF≌△FGE，则可证得AF=EF=AB，且∠EFA=∠FAB=90°，则可证得四边形ABEF为正方形．

试题解析：

（1）∵反比例函数（k＞0）的图象经过点D（3，1），∴k=3×1=3，∴反比例函数表达式为；

（2）①∵D为BC的中点，∴BC=2，∵△ABC与△EFG成中心对称，∴△ABC≌△EFG，∴GF=BC=2，GE=AC=1，∵点E在反比例函数的图象上，∴E（1，3），即OG=3，∴OF=OG﹣GF=1；

②如图，连接AF、BE，∵AC=1，OC=3，∴OA=GF=2，在△AOF和△FGE中，∵AO=FG，∠AOF=∠FGE，OF=GE，∴△AOF≌△FGE（SAS），∴∠GFE=∠FAO=∠ABC，∴∠GFE+∠AFO=∠FAO+∠BAC=90°，∴EF∥AB，且EF=AB，∴四边形ABEF为平行四边形，∴AF=EF，∴四边形ABEF为菱形，∵AF⊥EF，∴四边形ABEF为正方形．