题目内容
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°
(1)求证:△PAB∽△PBC
(2)求证:PA=2PC
(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3

【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)结合题意,易得∠ABC=45°=∠PBA+∠PBC,然后由∠APB=∠BPC=135°即可证明△PAB∽△PBC;
(2)根据(1)中△PAB∽△PBC,可得![]() ,然后由△ABC是等腰直角三角形,可得出
,然后由△ABC是等腰直角三角形,可得出![]() ,易得PA=2PC;
,易得PA=2PC;
(3)过点P作PD⊥BC,PE⊥AC交BC、AC于点D,E,首先由Rt△AEP∽Rt△CDP得出![]() ,即
,即![]() ,再根据△PAB∽△PBC可得出
,再根据△PAB∽△PBC可得出![]() ,整理即可得到
,整理即可得到![]() .
.
解:(1)∵∠ACB=90°,AC=BC,
∴∠ABC=45°=∠PBA+∠PBC
又∠APB=135°,
∴∠PAB+∠PBA=45°,
∴∠PBC=∠PAB,
又∵∠APB=∠BPC=135°,
∴△PAB∽△PBC;
(2)∵△PAB∽△PBC,
∴![]() ,
,
在Rt△ABC中,AC=BC,
∴![]() ,
,
∴![]()
∴PA=2PC;
(3)
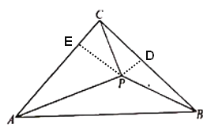
过点P作PD⊥BC,PE⊥AC交BC、AC于点D,E,
∵∠CPB+∠APB=135°+135°=270°,
∴∠APC=90°,∴∠EAP+∠ACP=90°,
又∵∠ACB=∠ACP+∠PCD=90°
∴∠EAP=∠PCD,
∴Rt△AEP∽Rt△CDP,
∴![]() ,即
,即![]() ,∴
,∴![]()
∵△PAB∽△PBC,
∴![]()
即![]() .
.

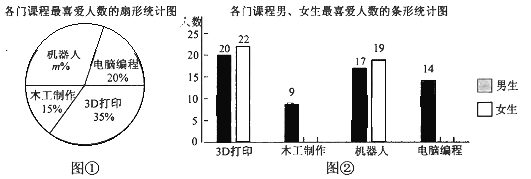
【题目】九(1)班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类别,每位同学仅选一项.根据调査结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | a | 0.5 |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | b | 1 |
根据图表提供的信息,回答下列问题:
(1)直接写出:a= .b= m= ;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请求选取的2人恰好是甲和乙的概率.

【题目】某商店新进一种台灯.这种台灯的成本价为每个30元,经调查发现,这种台灯每天的销售量y(单位:个)是销售单价x(单位:元)(30≤x≤60)的一次函数.
x | 30 | 35 | 40 | 45 | 50 |
y | 30 | 25 | 20 | 15 | 10 |
(1)求销售量y与销售单价x之间的函数表达式;
(2)设这种台灯每天的销售利润为w元.这种台灯销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?