题目内容
已知：关于x的方程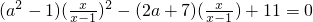
有实根．
（1）求a取值范围；
（2）若原方程的两个实数根为x1，x2，且
，求a的值．
解：设
=y，
①当方程为一次方程时，
即a2-1=0 a=±1．
②当方程为二次方程时，a2-1≠0
则a≠±1，
原方程可化为：（a2-1）y2-（2a+7）y+11=0，
∴△=b2-4ac=（2a+7）2-4（a2-1）×11≥0，
∴40a2-28a-93≤0，
解得：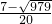
≤a≤
；
（2）设y1=
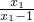，y2=
，
则y1，y2是方程（a2-1）y2-（2a+7）y+11=0的两个根，
∴y1+y2=
=
，
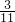解得：a=-
或a=10．
分析：（1）设=y，分两种情况讨论，①方程为一元一次方程，②方程为二元一次方程，那么有（a2-1）y2-（2a+7）y+11=0，根据△≥0即可求解；
（2）设y1=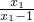，y2=，根据根与系数的关系即可求解．
点评：本题考查了根与系数的关系及根的判别式，属于基础题，关键是掌握根与系数之间的关系进行解题．
=y，①当方程为一次方程时，
即a2-1=0 a=±1．
②当方程为二次方程时，a2-1≠0
则a≠±1，
原方程可化为：（a2-1）y2-（2a+7）y+11=0，
∴△=b2-4ac=（2a+7）2-4（a2-1）×11≥0，
∴40a2-28a-93≤0，
解得：
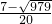≤a≤；（2）设y1=
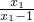，y2=，则y1，y2是方程（a2-1）y2-（2a+7）y+11=0的两个根，
∴y1+y2=
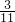=，解得：a=-
或a=10．分析：（1）设
=y，分两种情况讨论，①方程为一元一次方程，②方程为二元一次方程，那么有（a2-1）y2-（2a+7）y+11=0，根据△≥0即可求解；（2）设y1=
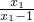，y2=，根据根与系数的关系即可求解．点评：本题考查了根与系数的关系及根的判别式，属于基础题，关键是掌握根与系数之间的关系进行解题．
练习册系列答案
考前必练系列答案
相关题目
有两个不相等的实数根（其中k为实数）。
有两个不相等的实数根（其中k为实数）. 
有两个不相等的实数根（其中k为实数）. 
有两个不相等的实数根（其中k为实数）。 
有两个不相等的实数根（其中k为实数）。